par Patrick » mer. 9 oct. 2013 16:00
Bonjour,
Voici un exercice sur le thème de la bijection associée à une fonction.
Même si les calculs sont basiques, la rédaction m'a posée des difficultés.
Soit \(f\) l'application définie sur \(\mathbb{R}\) et à valeurs dans \(\mathbb{R}\) :
\(f \quad:\quad x \mapsto y=x|x|\)
1) Démontrer que \(f\) est bijective de \(\mathbb{R}\) sur \(\mathbb{R}.\) Déterminer l'application réciproque \(f^{-1}\).
2) Tracer les courbes \(C_f\) et \(C_{f^{-1}}\) de \(f\) et \(f^{-1}\).
___________________________________________
1) Une application est bijective sur un intervalle ssi à chaque image \(y\) par \(f\) correspond un et un seul antécédent \(x\), ce qui revient à démontrer que l'équation :
(1)\(\quad y=x|x|\) admet une seule solution sur \(\mathbb{R}.\)
Sur \(\mathbb{R}_+\) on a : \(\left{ y=x^2\\ x\ge 0\right.\quad\Longleftrightarrow\quad\left{ x=\sqrt{y}\\ y\ge 0\right.\)
Sur \(\mathbb{R}_-\) on a : \(\left{ y=-x^2\\ x\lt 0\right.\quad\Longleftrightarrow\quad\left{ x=-\sqrt{-y}\\ y\lt 0\right.\)
L'équation (1) admet donc une seule solution sur \(\mathbb{R}\) car la fonction racine est bijective sur son intervalle de définition. CQFD ?
L'expression de l'application réciproque \(f^{-1}\) s'obtient en échangeant les rôles de \(x\) et de \(y\ :\)
Sur \(\mathbb{R}_+\) on a : \(\left{ y=\sqrt{x}\\ y\ge 0\right.\) et sur \(\mathbb{R}_-\) on a : \(\left{ y=-\sqrt{-x}\\ y\lt 0\right.\quad\) CQFD ?
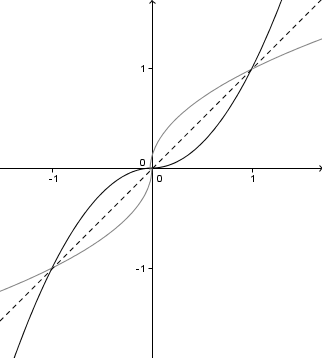
2) J'ai tracé, à l'aide de GeoGebra, les courbes \(C_f\) (en noir) et \(C_{f^{-1}}.\) (en gris). En plus, j'ai représenté la 1ère bissectrice pour mettre en évidence la symétrie des courbes.
J'attends vos remarques, Merci d'avance.
@+
- Fichiers joints
-
- Illustration réalisée avec GeoGebra
- Courbes.png (10 Kio) Vu 1499 fois
Bonjour,
Voici un exercice sur le thème de la bijection associée à une fonction.
Même si les calculs sont basiques, la rédaction m'a posée des difficultés.
Soit [tex]f[/tex] l'application définie sur [tex]\mathbb{R}[/tex] et à valeurs dans [tex]\mathbb{R}[/tex] :
[tex]f \quad:\quad x \mapsto y=x|x|[/tex]
1) Démontrer que [tex]f[/tex] est bijective de [tex]\mathbb{R}[/tex] sur [tex]\mathbb{R}.[/tex] Déterminer l'application réciproque [tex]f^{-1}[/tex].
2) Tracer les courbes [tex]C_f[/tex] et [tex]C_{f^{-1}}[/tex] de [tex]f[/tex] et [tex]f^{-1}[/tex].
___________________________________________
1) Une application est bijective sur un intervalle ssi à chaque image [tex]y[/tex] par [tex]f[/tex] correspond un et un seul antécédent [tex]x[/tex], ce qui revient à démontrer que l'équation :
(1)[tex]\quad y=x|x|[/tex] admet une seule solution sur [tex]\mathbb{R}.[/tex]
Sur [tex]\mathbb{R}_+[/tex] on a : [tex]\left{ y=x^2\\ x\ge 0\right.\quad\Longleftrightarrow\quad\left{ x=\sqrt{y}\\ y\ge 0\right.[/tex]
Sur [tex]\mathbb{R}_-[/tex] on a : [tex]\left{ y=-x^2\\ x\lt 0\right.\quad\Longleftrightarrow\quad\left{ x=-\sqrt{-y}\\ y\lt 0\right.[/tex]
L'équation (1) admet donc une seule solution sur [tex]\mathbb{R}[/tex] car la fonction racine est bijective sur son intervalle de définition. CQFD ?
L'expression de l'application réciproque [tex]f^{-1}[/tex] s'obtient en échangeant les rôles de [tex]x[/tex] et de [tex]y\ :[/tex]
Sur [tex]\mathbb{R}_+[/tex] on a : [tex]\left{ y=\sqrt{x}\\ y\ge 0\right.[/tex] et sur [tex]\mathbb{R}_-[/tex] on a : [tex]\left{ y=-\sqrt{-x}\\ y\lt 0\right.\quad[/tex] CQFD ?
2) J'ai tracé, à l'aide de GeoGebra, les courbes [tex]C_f[/tex] (en noir) et [tex]C_{f^{-1}}.[/tex] (en gris). En plus, j'ai représenté la 1ère bissectrice pour mettre en évidence la symétrie des courbes.
J'attends vos remarques, Merci d'avance.
@+