Page 1 sur 1
Coniques exo 4)
Posté : sam. 3 mars 2018 19:39
par Antony
Bonsoir,
Alors pour le 4) je rencontre de la difficulte je sais que c’est une hyperbole.
Mais pour trouver l’equation à l’aide du contexte aucune idée.
Merci de votre aide.
Re: Coniques exo 4)
Posté : sam. 3 mars 2018 20:10
par SoS-Math(9)
Bonsoir Antony,
Comme pour la parabole, place sur une figure tes foyers F et F', tes sommets S et S' et utilise le fait que |SF - SF'|= 40.
SoSMath.
Re: Coniques exo 4)
Posté : sam. 3 mars 2018 20:31
par Antony
Dans le corrige Le prof dit que les foyers sont (29,0) et (-29,0)
Mais je comprends pas pourquoi et 2a=40 a=20
Je comprends toujours pas comment faire pour savoir cela.
Merci de votre aide
Re: Coniques exo 4)
Posté : sam. 3 mars 2018 20:33
par Antont
C’est pour cela que pour tracer le graphique pour ce numéro aucune idée puisqu’en je comprends pas comment trouver les paramètres meme son je vous ai Dian les réponses plus tôt
Re: Coniques exo 4)
Posté : sam. 3 mars 2018 21:03
par SoS-Math(9)
Antony,
As-tu fait une figure ?
En principe avec la figure, on constate que |SF - SF'|= SS' = 2a or |SF - SF'|= 40 donc 2a = 40 ...
SoSMath.
Re: Coniques exo 4)
Posté : sam. 3 mars 2018 21:14
par Antony
Non car je ne sais pas comment dessiner l’équation puisque je comprends pas la technique pour trouver la regle sachant que c’est
x^2/a^2 - y^2/b^2=1
Re: Coniques exo 4)
Posté : sam. 3 mars 2018 21:36
par SoS-Math(9)
Anthony,
voici une figure :
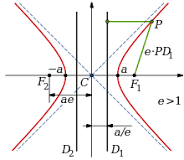
- Hyperbole.png (11.17 Kio) Vu 5265 fois
SoSMath.
Re: Coniques exo 4)
Posté : sam. 3 mars 2018 21:52
par Antony
Ca c’est un genre de numéro que s’il y a ça dans mon examen que je rate.
Si le foyer =( -29,0) et (29,0)
Ca veut dire qu’en s’il nous donnera le point a ils auraient dit simplement (-29,0) comme dans les autres problèmes qu’en j’avais posté ici précédemment?
Donc a=29 donc ce ne serais pas le foyer?
Après pour trouver le paramètre a puisque c’est égal à 1 graphiquement je ne vois pas comme faire -ce que ou il y a la ligne des x distance entre les sommet (a,0) et (-a,0)=40
Ce qui donne
2a=40
a=20?
Merci de votre aide.
Re: Coniques exo 4)
Posté : sam. 3 mars 2018 23:27
par Antony
La j’ai compris.
Merci de votre aide
Re: Coniques exo 4)
Posté : dim. 4 mars 2018 09:59
par SoS-Math(33)
Bonne journée
SoS-math