Bonjour,
M --> M'
\(\overrightarrow{MM'} = \overrightarrow{MA} - 2\times \overrightarrow{MB} + \overrightarrow{MC}\)
B --> D
\(\overrightarrow{BD} = \overrightarrow{BA} - 2\times \overrightarrow{BB} + \overrightarrow{BC}\)
\(\overrightarrow{BD} = \overrightarrow{BA} - 2 \times\overrightarrow{0} + \overrightarrow{BC}\)
\(\overrightarrow{BD} = \overrightarrow{BA} + \overrightarrow{BC}\)
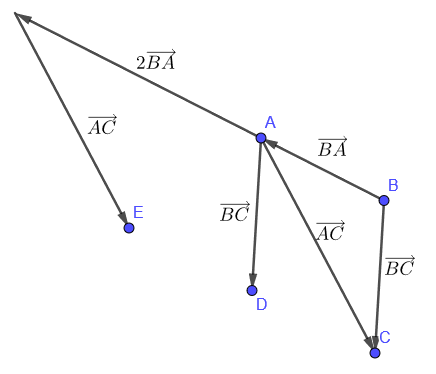
A --> E
\(\overrightarrow{AE} = \overrightarrow{AA} - 2\times \overrightarrow{AB} + \overrightarrow{AC}\)
\(\overrightarrow{AE} = \overrightarrow{0} - 2\times \overrightarrow{AB} + \overrightarrow{AC}\)
\(\overrightarrow{AE} = 2\times \overrightarrow{BA} + \overrightarrow{AC}\)
- vect.PNG (10.7 Kio) Vu 4203 fois
Est-ce plus clair?
SoS-math