Page 1 sur 1
limites
Posté : dim. 13 sept. 2009 13:47
par similliri
bonjour
voici la fonction
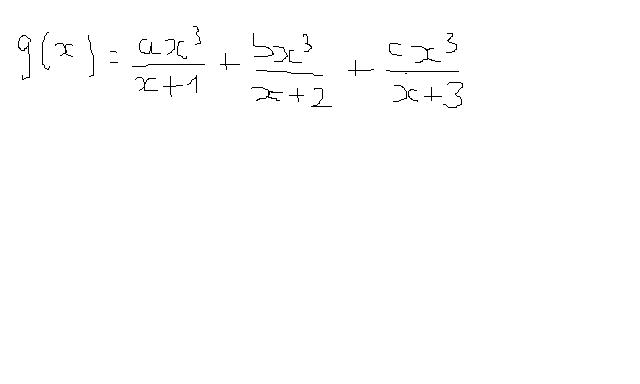
- Sans titre.jpg (10.36 Kio) Vu 2434 fois
Je ne sais pas comment prouver qu'il y a trois asymptotes verticales
pouvez vous me répondre rapidement ?
Merci
Re: limites
Posté : dim. 13 sept. 2009 15:06
par SoS-Math(11)
Rapidement : regarde les dénominateurs
Re: limites
Posté : dim. 13 sept. 2009 15:11
par sos-math(12)
Bonjour similliri :
Il te faut revenir à la propriété permettant d'affirmer qu'une courbe admet une asymptote verticale. Tu as placé ton énoncé dans le sujet limites donc tu dois savoir qu'il existe un lien entre l'existence d'une asymptot verticale et les limites de la fonction étudiée.
Tu peux aussi essayer de visualiser la représentation graphique de la fonction \(g(x)=\frac {x^3}{x+1}+\frac {x^3}{x+2}+\frac {x^3}{x+3}\) à l'aide d'une calculatrice ou d'un grapheur pour emettre des conjectures et essayer ensuite de les valider.
Bonne chance et à bientôt.
Re: limites
Posté : dim. 13 sept. 2009 18:32
par similliri
Bonjour
la propriété est que la droite d'équation x=a ssi lim f quand x-->a- =+ou- infini ou lim f quand x-->a+=+ou- infini
Mais même avec cela je n'y arrive pas puique je ne sais pas vers quoi tend x.
Pouvez vous m'aider ?
Merci d'avance.
Re: limites
Posté : dim. 13 sept. 2009 20:11
par sos-math(13)
Bonsoir,
essaie de soigner tes messages, en n'oubliant pas la moitié des phrases, sinon cela devient très dur de communiquer.
Pour le reste, si tu veux une limite qui tende vers l'infini, il va falloir un dénominateur qui tend vers 0... Donc, en observant tes dénominateurs, tu peux voir simplement vers quoi doit tendre x.
Bon courage.