SOS-MATH

Bonjour, j'aurais besoin d'aide pour 3 questions en tout auxquelles j'ai du mal à répondre dans mon devoir maison. Pouvez vous m'aider. Merci d'avance.

Bonjour,
tu peux toujours poser tes questions, nous tâcherons d'y répondre mais n'oublie pas que tu dois faire ce devoir maison toute seule....
À bientôt

Re bonjour, voila
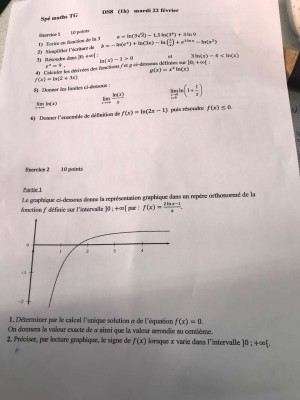
Exercice 2 :

Partie I

1. Je crois que je dois utilisés a/b =0 ?

2.

Partie II

1.a et 1.b 2. 3.

Bonjour,
j'ai l'impression qu'on a déjà répondu à cette demande : on a déjà parlé des limites, il me semble ainsi que des variations.
Quelle est ta demande précisément ?

Bonjour, j'ai besoin de savoir si la question 2 de la partie I est juste, je n'arrive pas a répondre a la 1 ainsi qu'au question 4 et 5 de la Partie 2.
Merci

On a déjà réglé la partie 1, non ?
Remonte les messages du sujet et tu verras qu'on a clos le débat.
Pour les variations, il te manque l'image de \(g(\sqrt{e})\) et ton tableau sera complet, ce qui te servira pour le 4.
Pour le 4, il s'agit d'appliquer le théorème des valeurs intermédiaires au deux intervalles de variation pour vérifier que l'équation \(g(x)=m\) admet une unique solution sur chacun de ces intervalles de variation.
Connais-tu ce théorème ?

Pour la partie I, Je n'ai toujours pas réussi a répondre a la première question et je ne sas toujours pas si la 2ème question est juste

Pour la Partie II, j'ai calculée l'image de g(racine(e)) = -0,25

question 4 : Merci

Bonsoir Céline,

Il est inutile de posté plusieurs fois ton message ... on essaye de répondre aussi vite que possible.

Pour la partie I, je te renvoie au sujet déjà traité : http://sosmath.ac-poitiers.fr/viewtopic.php?f=9&t=20467.

Pour la partie II, question 4, pour moi g(1) = (ln(1))^2 - ln(1) = 0 et non 1. Il faut utiliser l'intervalle ]0 ; \(\sqrt{e}\) ]

tu sais que f est strictement décroissante et continue sur ]0 ; \(\sqrt{e}\) ] et de plus g(\(\sqrt{e}\))=-0,25 et \(\lim_{x \to 0} g(x)=+\infty\), donc d'après le TVI, si m > -0,25, il existe une unique solution à l'équation g(x) = m, comprise entre 0 et \(\sqrt{e}\)

Il faut faire la même chose sur [\(\sqrt{e}\) ; +\(\infty\)]

SoSMath.

Merci beaucoup, j’ai compris et je l’ai fais pour la partie croissante. Maintenant comment calculer les deux solutions (question 5).

Bonjour,
pour résoudre \(g(x)=0\), tu dois factoriser \(g(x)\) de sorte à avoir \(\ln(x)\times(\ln(x)-1)=0\).
Tu te retrouves alors avec une équation de type "produit-nul" :
Un produit de deux facteurs est nul lorsqu'au moins un des deux facteurs est nul
donc si tu as \(A\times B=0\) alors tu dois avoir \(A=0\) ou \(B=0\).
Cela va te faire deux équations à résoudre et tu auras alors les solutions.
Bonne résolution