Page 1 sur 1
Integral
Posté : sam. 2 mai 2020 16:44
par Yessine
Bonjour,
Ex:
Calculer
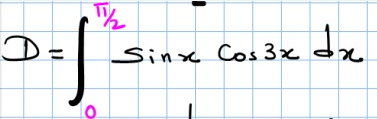
- 1.png (41.84 Kio) Vu 1409 fois
Correction:
je ne comprends pas cette étape :
sin(x)*cos(3x) = (1/2)*(sin(4x)-sin(2x))
pouvez vous m'aider?
Merci d'avance
Re: Integral
Posté : sam. 2 mai 2020 19:50
par sos-math(21)
Bonjour,
il s'agit des fameuses formules trigonométriques qui permettent de transformer des produits en somme ou inversement :
voir formulaire produit/somme du la page suivante :
https://fr.wikiversity.org/wiki/Trigonom%C3%A9trie/Relations_trigonom%C3%A9triques
En particulier, on utilise celle-ci : \(\cos(a)\sin(b)=\dfrac{1}{2}\left(\sin(a+b)-\sin(a-b)\right)\)
donc en prenant \(a=3x\) et \(b=x\), on a \(\sin(x)\cos(3x)=\cos(3x)\sin(x)=\dfrac{1}{2}\left(\sin(3x+x)-\sin(3x-x)\right)=\dfrac{1}{2}\left(\sin(4x)-\sin(2x)\right)\)
Bonne continuation