Page 1 sur 1
Problème ouvert : géométrie, fonctions, trigonométrie...
Posté : jeu. 29 déc. 2016 13:17
par Anaëlle
Bonjour tout le monde, vous allez bien ?
Alors j'ai un DM facultatif de maths à rendre mais je galère, j'aimerais que vous me donniez un point de départ (vous n'allez pas faire tout le boulot).
Alors, le problème se nomme: égalité d'aire.
On considère la figure ci-dessous, sur laquelle le centre du secteur circulaire est le sommet du triangle isocèle vert.
Pour quelle(s) valeur(s) l'angle d'ouverture du secteur circulaire les aires des parties rose et verte sont-elles égales ?
Re: Problème ouvert : géométrie, fonctions, trigonométrie...
Posté : jeu. 29 déc. 2016 14:51
par sos-math(21)
Bonjour,
pour commencer, je te propose de nommer certaines inconnues.
Tu peux appeler \(x\) le rayon du cercle de sorte que la base de ton triangle isocèle soit \(2x\).
Tu peux ensuite appeler \(h\) la hauteur issue du sommet principal. Tu peux aussi appeler \(\theta\) la demi-mesure de l'angle du sommet principal comme sur le schéma ci-dessous :
Tu peux ensuite exprimer \(\theta\) en fonction de \(x\) et \(h\)
Je te conseille ensuite d'exprimer en fonction de \(h\) et \(x\) l'aire des deux surfaces.
Tu dois aboutir à une équation d'inconnue \(\theta\)
Bon courage
Re: Problème ouvert : géométrie, fonctions, trigonométrie...
Posté : jeu. 29 déc. 2016 16:09
par Anaëlle
Merci infiniment, vous avez été très clair dans vos explications.
J'ai juste quelques questions (désolée), j'ai suivi ce que vous m'avez conseillé et j'ai abouti à:
Pour θ en fonction de x et de h j'ai trouvé:
tanθ= x/h
Ensuite pour l'aire du triangle rectangle, je suis arrivée à:
A= (h*x)/2
Enfin pour l'aire du demi-cercle j'ai:
A= (1/2)xπxr²
A ce stade, je ne vois pas encore comment aboutir à l'équation d'inconnue θ.
Pourriez-vous de nouveau m'aider s'il vous plaît ?
Re: Problème ouvert : géométrie, fonctions, trigonométrie...
Posté : jeu. 29 déc. 2016 16:32
par SoS-Math(33)
Bonjour Anaëlle,
attention la partie verte est le double du triangle rectangle.
Pour la partie rose tu es sure que c'est un demi cercle? tu devrais peut être utiliser la formule du calcul de l'aire d'un secteur circulaire.
Re: Problème ouvert : géométrie, fonctions, trigonométrie...
Posté : lun. 2 janv. 2017 11:33
par Anaëlle
Bonjour,
Alors j'ai corriger les fautes que j'avais faite et j'ai donc obtenu:
Aire du triangle rectangle: h*x
Aire du secteur circulaire: ((2π*r²)/360°)*θ°
Le rayon ne nous est pas donné, au départ j'avais pensé à h sauf qu'il ne va pas jusqu'au bout de la figure donc on en peut pas le considérer comme rayon et ainsi je ne vois pas comment finir de remplacer les expressions littérales par des expressions numériques.
Re: Problème ouvert : géométrie, fonctions, trigonométrie...
Posté : lun. 2 janv. 2017 11:55
par SoS-Math(33)
Bonjour,
tu peux exprimer x et h en fonction de r et de \(\theta\) en utilisant les formules de trigonométrie
Re: Problème ouvert : géométrie, fonctions, trigonométrie...
Posté : lun. 2 janv. 2017 12:44
par Anaëlle
Est-ce que ce sont les formules trigonométriques de base (CAHSOHTOA) qu'il faut utiliser ou d'autres plus spécifiques ? Car je ne parviens pas à exprimer x et h en fonction de r et de θ.
Merci
Re: Problème ouvert : géométrie, fonctions, trigonométrie...
Posté : lun. 2 janv. 2017 12:57
par SoS-Math(33)
Oui c'est sin, cos et tan
Ton r est bien l'hypoténuse du triangle rectangle?
Si c'est le cas tu dois utiliser sin pour x et cos pour h
Je te laisse faire les calculs
Re: Problème ouvert : géométrie, fonctions, trigonométrie...
Posté : lun. 2 janv. 2017 14:34
par Anaëlle
Et si ce n'est pas le cas ?
Parce que pour moi l'hypoténuse est un côté que je n'ai pas nommé et il n'y a aucun côté qui peut être rayon puisque aucun ne va jusqu'au bout.
Re: Problème ouvert : géométrie, fonctions, trigonométrie...
Posté : lun. 2 janv. 2017 14:48
par SoS-Math(33)
Bonjour,
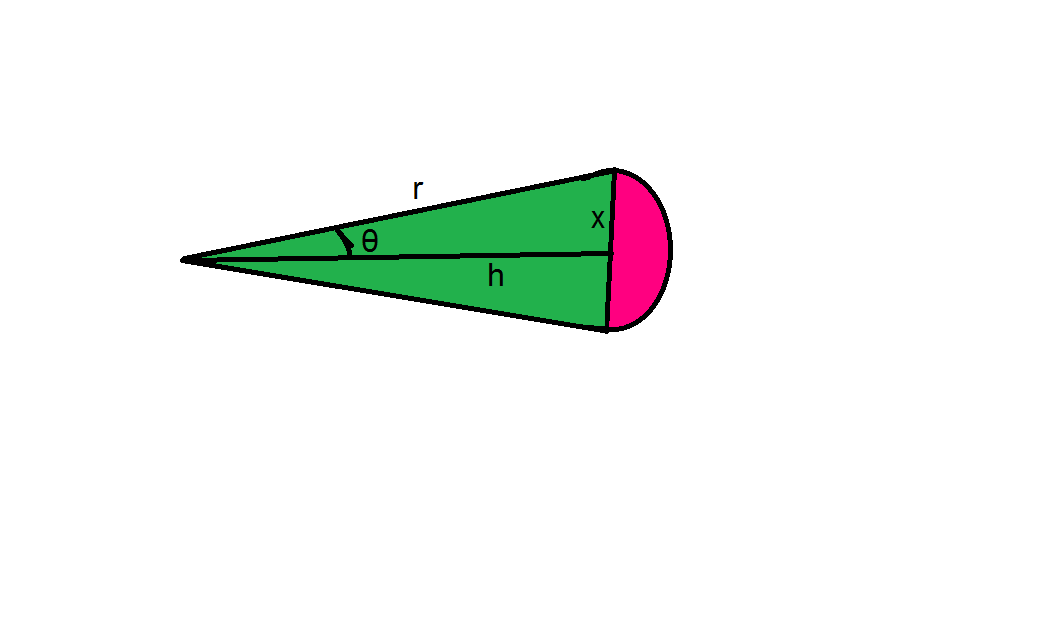
- Sans titre.png (7.25 Kio) Vu 6707 fois
Sur le schéma r est le rayon du secteur circulaire, ensuite tu peux relier \(\theta\) avec x et r par le sinus ET avec h et r par le cosinus
Re: Problème ouvert : géométrie, fonctions, trigonométrie...
Posté : lun. 2 janv. 2017 23:12
par Anaëlle
Ah ben très bien, je ne voyais pas ça comme ça merci infiniment à vous et à l'autre modérateur de m'avoir aider. Bonne soirée et bonne année !!
Re: Problème ouvert : géométrie, fonctions, trigonométrie...
Posté : mar. 3 janv. 2017 12:53
par sos-math(21)
Bonjour,
merci pour ton message de remerciements.
Bonne continuation