Page 1 sur 2
suite
Posté : sam. 5 sept. 2015 19:06
par pierre
bonjour,
soit ( \(\ u_{n}\) ) la suite definie par :U0=5, U1=2 et la relation \(\ u_{n+2}\) = 3\(\ u_{n+1}\) + 4\(\ u_{n}\)
1.Déterminer les solutions α et ß de l'équation X²=3X+4
2. soit ( \(\ V_{n}\) ) et ( \(\ w_{n}\) ) les suites definies pour tout entier naturel n par: \(\ V_{n}\) = \(\ u_{n+1}\) - α \(\ u_{n}\) et \(\ w_{n}\)= \(\ u_{n+1}\) - ß \(\ u_{n}\)
a) determiner l'expression de \(\ V_{n}\) puis celle de \(\ w_{n}\) en fonction de n
b) en deduire l'expression de \(\ u_{n}\) en fonction de n
J'ai trouvé ß= -6.25 α=-1.5
je bloque pour le reste j'ai trouvé \(\ u_{n+1}\) = (4 \(\ u_{n}\) - \(\ u_{n+2}\) ) / 3
pouvez vous s'il vous plait m'aider
Re: suite
Posté : sam. 5 sept. 2015 21:41
par sos-math(21)
Bonjour,
Résoudre l'équation \(x^2=3x+4\) revient à résoudre \(x^2-3x-4=0\) et les solutions obtenues ne sont pas égales à -6.25 et -1.5.
Reprends déjà cela, tu feras un meilleur départ dans cet exercice.
Bon courage
Re: suite
Posté : dim. 6 sept. 2015 08:09
par pierre
bonjour,
j'ai refait le calcul de x²-3x-4=0
je trouve alpha=1.5 et beta=-6.25 est ce exacte
comment faire la suite car on ne connait ni Un ni Un+1 afin de determiner Vn et Wn en fonction de n
Re: suite
Posté : dim. 6 sept. 2015 13:17
par pierre
bonjour, merci de votre réponse
j'ai recalculé Béta et Alpha je trouve: Beta= -6.25 et Alpha=1.5
2)A) Vn=Un+1-1.5Un+1
Wn=Un+1+(25/4)Un
Est ce bon? Comment en déduire l'expression de Un ? SVP
Merci
Re: suite
Posté : dim. 6 sept. 2015 14:13
par sos-math(21)
Bonjour,
je ne suis toujours pas d'accord :
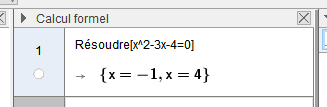
- resol_equation.png (2.42 Kio) Vu 5602 fois
Détaille ta résolution pour que nous trouvions ton erreur.
Bonne continuation
Re: suite
Posté : dim. 6 sept. 2015 14:39
par pierre
Il faut déterminer les solutions de Alpha et Beta
J'ai fait:
Alpha= -b/2a soit: Alpha= 3/2
Béta= -Delta/4a soit : Béta=-25/4
est ce bon?
SVP Merci
Re: suite
Posté : dim. 6 sept. 2015 14:44
par sos-math(21)
Pierre,
je te conseille de revoir tes formules de résolutions d'une équation du second degré.
Cela devrait aller mieux après.
Bonne continuation
Re: suite
Posté : dim. 6 sept. 2015 15:03
par pierre
j'ai resolue selon le théorème du trinome du second degre de la forme f(x)=ax²+bx+c (avec a pas egale à 0)
s'écrit sous la forme canonique f(x)=a(x-alpha)²+ beta avec alpha= -b/2a et beta= f(alpha
Re: suite
Posté : dim. 6 sept. 2015 16:18
par sos-math(21)
Pierre,
ce n'est pas cette formule qui te permet de résoudre l'équation \(x^2-3x-4=0\).
Il faut que tu calcules le discriminant : \(\Delta=b^2-4ac\) et, celui-ci étant positif, tu auras deux solutions :
\(x_1=\frac{-b-\sqrt{\Delta}}{2a}\) et \(x_2=\frac{-b+\sqrt{\Delta}}{2a}\).
Je te laisse reprendre cela....
Re: suite
Posté : lun. 7 sept. 2015 06:11
par pierre
bonjour
merci ^pour l'aide j'étais parti sur la forme canonique c'est le beta et l'alpha qui m'a perdu
j'ai refais le calcul et trouve x1=-1 et x2=4
donc alpha=-1 et beta=4
Soit (Vn) et (Wn) les suites definies pour tout entier naturel n par : Vn=Un+1-alphaUn et Wn=Un+1-betaUn
determiner l'expression de Vn puis celle de Wn en fonction de n
en deduire l'expression de Un en fonction de n
j'ai fait Vn=Un+1+Un et Wn=Un+1-4Un
Vn= (Un)(U1+1) soit 3Un
Wn=Un(U1-4) soit Wn=-2Un
ensuite 3Un=Un+1+Un Un+1=2Un
-2Un=Un+1-4Un
Un+1=2Un
est ce ce qu'il faut faire sinon pouvez vous m'indiquer la voie
merci beaucoup
bonne journée
Re: suite
Posté : lun. 7 sept. 2015 11:20
par sos-math(21)
Bonjour,
les suites que l'on définit vont être particulières.
Par exemple \(v_n=u_{n+1}+u_n\)
Si on regarde au rang \(n+1\), on a \(v_{n+1}=u_{n+2}+u_{n+1}=\underbrace{3u_{n+1}+4u_{n}}_{=u_{n+2}}+u_{n+1}\) ce qui donne \(v_{n+1}=4u_{n+1}+4u_n=4(...+...)=4\times ...\) ce qui prouve que ta suite \((v_n)\) est .... de raison ...
Et tu auras ensuite avec ton cours une expression de \(v_n\) en fonction de \(n\).
Je te laisse poursuivre
Re: suite
Posté : lun. 7 sept. 2015 20:53
par pierre
bonsoir
j'ai marqué
ce qui prouve que Vn est geomètrique de raison 4
Vn=V0xq^n
Vn=7x4^n
j'ai calculé W+1 et trouvé 2Un ai je le droit de faire -Un+4Un=-UnxU1+4Un=-2Un+4Un
ce qui prouve de Wn est geomètrique de raison 2
W0=-18x2^n
en deduire Un en fonction de n
U0=5 U1=2 x²-3x-4=0
x1=-1 x2=4
Un=a+d4^n
a+b=5
-a+4b=2
b=5-a
-a+4x5-a=2
a=18/5
b=5-(18/5)
b= 7/5
Pour conclure Un= (18/5)+(4x(7/5)^n)
Un=(15/5)+(28/5)^n
Mais résultats sont ils exactes merci pour les réponses SVP
Re: suite
Posté : lun. 7 sept. 2015 21:12
par sos-math(28)
Bonsoir
Il faut revoir les calculs pour la suite \(\left(w_n\right)\) .
Il faut comme pour la suite \(\left(v_n\right)\) calculer \(w_{n+1}\) en fonction de \(w_{n}\)
Bon courage
Re: suite
Posté : mar. 8 sept. 2015 06:14
par pierre
bonjour
j'ai bien fais le calcul de Wn+1
Wn=Un+1-4Un
Wn+1=Un+2-4Un+1
Wn+1=3Un+1+4Un-4Un+1
Wn+1=-Un+1-4Un
ensuite j'avais factorisé par Un mais j'ai un doute, je ne sais pas si j'ai le droit
j'ai refais le calcul et je retrouve Wn+1=-Un+1+4Un
comment faire la suite
et pour deduire l'expression de Un en fonction de n?
merci bonne journée
Re: suite
Posté : mer. 9 sept. 2015 06:01
par pierre
bonjour
je dois rendre mon dmdemain et je suis bloqué au calcul de Wn
j'aicalculé Wn+1=Un+2-4Un+1
Wn+1=3Un+1+4UN-4Un+1=-Un+1+4Un
comment le factoriser
puis comment en deduire Un en fonction de n
MERCI DE VOTRE REPONSE