Page 1 sur 1
aritmetique
Posté : jeu. 5 févr. 2015 01:06
par ulrich
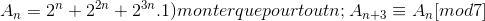
- pb
- CodeCogsEqn.gif (1.71 Kio) Vu 2053 fois
slt grand pardon je n'arrive pa a faire ceci.aidé moi
Re: aritmetique
Posté : jeu. 5 févr. 2015 11:09
par sos-math(20)
Bonjour Ulrich,
Nous tenons à ce que les utilisateurs du forum fassent preuve de politesse : "bonjour" et "merci" sont les bienvenus lorsque vous posez une question.
De plus, le but de ce forum est de vous aider à trouver la solution mais pas de faire le travail à votre place.
Veuillez reformuler votre demande en nous expliquant ce que vous avez déjà fait.
A bientôt sur SOS-math
Re: aritmetique
Posté : mer. 11 févr. 2015 00:09
par ulrich
slt grand.c'es la premiere kestion et j'ai pensé a faire la recurence mais les A me gène.pardon aiderv moi.merci
Re: aritmetique
Posté : mer. 11 févr. 2015 07:23
par sos-math(21)
Bonjour,
Visiblement vous n'avez pas compris le sens du message que l'on vous a envoyé.
Nous attendons une nouvelle version de votre demande.
Pour commencer, commencez par écrire ce que vaut \(A_{n+3}=2^{n+3}+....\) et faites "ressortir" les éléments définissant \(A_n\) : les facteurs seront des nombres qui ont une congruence intéressante modulo 7.
Bonne journée
Sos-math
Re: aritmetique
Posté : ven. 20 févr. 2015 22:32
par ulrich
bsr grand j'ai reusit a trouvé.apres avoir trouvé les restes de la division de de \(2^{n}\) par 7 et montrer ke
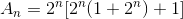
- CodeCogsEqn (1).gif (678 Octets) Vu 2027 fois
on demande de determiner les entiers n tel que An soit divisible par 7(on poura etudier les cas n=3k;n=3k+1;n=3k+2).je ne sai quoi faire.merci
Re: aritmetique
Posté : sam. 21 févr. 2015 11:11
par SoS-Math(9)
Bonjour Ulrich,
Il faut commencer par déterminer les restes de \(2^{3k}\) par 7, puis ceux de \(2^{3k+1}\) et \(2^{3k+2}\).
Et ensuite les utiliser dans ton expression : \(A_n=2^n(2^n(1+2^n)+1)\).
SoSMath.
Re: aritmetique
Posté : dim. 22 févr. 2015 19:11
par ulrich
slt grand.pour les reste de la division je trouve respectivement 1,2,4.comment les utiliser dans mon expression,.merci
Re: aritmetique
Posté : dim. 22 févr. 2015 21:15
par SoS-Math(9)
Ulrich,
Il faut utiliser les règles de calcul sur les congruences ...
pour n = 3k
2^3 = 8
donc \(2^3=8\equiv 1 [7]\)
donc \((2^3)^k=2^{3k}\equiv 1^k [7]\)
soit \(2^{3k}\equiv 1 [7]\).
Avec cela tu dois, pouvoir montrer que \(A_{3k}\equiv 3 [7]\).
Je te laisse terminer.
SoSMath.