Page 1 sur 2
Fonction exponentielle
Posté : sam. 13 déc. 2014 16:33
par Alice term s
Bonjour,
Je m'entraîne actuellement sur un sujet de bac mais je suis bloquée à une question, je ne vois pas où est mon erreur: Il s'agit de la 4.a. voici ce que j'ai fait:
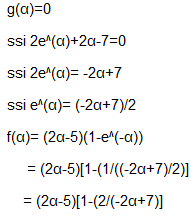
- Exp.png (4.1 Kio) Vu 7685 fois
Je ne trouve pas le bon résultat en poursuivant. Je pense que c'est une erreur de signe.
Voici le sujet:
Merci d'avance.
Re: Fonction exponentielle
Posté : sam. 13 déc. 2014 16:58
par SoS-Math(9)
Bonjour Alice,
ton travail est correct ... il faut continuer à simplifier ton calcul !
Tu as : \(1-\frac{2}{-2\alpha + 7} = \frac{-2\alpha + 7}{-2\alpha + 7} - \frac{2}{-2\alpha + 7} = ...\)
Je te laisse continuer.
SoSMath.
Re: Fonction exponentielle
Posté : sam. 13 déc. 2014 20:17
par Alice term s
Merci de votre réponse.
Ai-je le droit de faire:
\(\frac{-2a+5}{-2a+7}\)=\(\frac{2a-5}{2a-7}\) ?
Car sinon je vois pas comment poursuivre.
Merci d'avance.
Re: Fonction exponentielle
Posté : sam. 13 déc. 2014 21:01
par SoS-Math(9)
Bien sur Alice !
tu as le droit de multiplier par même nombre (ici -1) le numérateur et le dénominateur d'une fraction.
SoSMath.
Re: Fonction exponentielle
Posté : sam. 13 déc. 2014 22:49
par Alice term s
Merci, j'avais un doute...
Par contre, je suis totalement bloquée à la partie c, je vois pas comment démarrer du tout...
Merci d'avance.
Re: Fonction exponentielle
Posté : dim. 14 déc. 2014 09:11
par sos-math(21)
Bonjour,
Je ne vois pas de partie C dans ton sujet : ce que tu nous as envoyé s'arrête à la partie B.
Merci de préciser la suite.
Re: Fonction exponentielle
Posté : dim. 14 déc. 2014 14:59
par Alice term s
Bonjour,
Ah oui excusez-moi, je n'ai pas fait attention, la voici, c'est la partie D:
Merci d'avance.
Re: Fonction exponentielle
Posté : dim. 14 déc. 2014 18:24
par sos-math(21)
Il faut que tu calcules les longueurs suivantes :
\(C_nB_n\) et \(A_nB_n\).
Tous ces points ont la même abscisse \(n\) donc calculer les longueurs revient à faire la différence (positive) entre leurs ordonnées.
J'imagine que tu as montré auparavant que \(\mathscr{C}\) était en-dessous de \(\mathscr{D}\) de sorte que \(C_nB_n=y_{C_n}-y_{B_n}\).
De même, la droite \(\mathscr{D}\) est au-dessus de l'axe des abscisses à l'abscisse \(n\) donc \(A_nB_n=y_{B_n}-y_{A_n}\).
Je te laisse terminer pour retrouver l'expression proposée.
Bonne continuation
Re: Fonction exponentielle
Posté : dim. 14 déc. 2014 20:46
par Alice term s
Merci de votre réponse. Cependant, je ne comprends pas la démarche à suivre. Je ne comprends pas le lien pour la différence des ordonnées avec le fait d'avoir étudié les positions relatives précédemment.
Merci d'avance.
Re: Fonction exponentielle
Posté : dim. 14 déc. 2014 21:17
par sos-math(21)
Les positions relatives te permettent de faire les différences d'ordonnées dans le bon sens afin d'avoir des valeurs positives qui correspondent bien à une longueur :
Si tu as A(5 ; 6) et B(5 ; 2) : comme A et B ont la même abscisse, AB correspond à la différence entre les ordonnées : (la plus grande) - (la plus petite).
Donc \(6-2\) et non pas \(2-6\) : on a donc bien besoin de savoir la position relative pour faire la différence dans le bon sens.
Re: Fonction exponentielle
Posté : dim. 14 déc. 2014 21:32
par Alice term s
Ah d'accord, je comprends. Et Ybn, c'est l'équation de la droite D ? Et Ycn celle de f(x) ? En fait, je trouve ça bizarre dans le sens où j'ai pas de valeurs que je peux appliquer numériquement. Autant les parties précédentes du sujet me paraîssaient assez classiques, autant celle-ci me perturbe.
Merci d'avance.
Re: Fonction exponentielle
Posté : dim. 14 déc. 2014 21:34
par sos-math(21)
Ce sont les ORDONNÉES des points !
Reprends cela
Re: Fonction exponentielle
Posté : dim. 14 déc. 2014 21:41
par Alice term s
Pour Ycn, pour connaître son ordonnée, je fais f(n) soit f(n)=(2n-5)(1-e^(-x)), et pour Ybn, je fais 2n-5 ?
Merci d'avance.
Re: Fonction exponentielle
Posté : lun. 15 déc. 2014 16:19
par sos-math(27)
Bonjour,
Ce sont les bonnes expressions, il ne faut pas de tromper en faisant la différence, elle doit être positive..
Bonne continuation
Re: Fonction exponentielle
Posté : lun. 15 déc. 2014 20:50
par Alice term s
Bonsoir,
J'ai réussi cette question mais je bloque pour la suivante, la 2.a. Faut-il que je calcule U1 et U2 et qu'ensuite je fasse le quotient et la différence pour se donner une idée avant de prouver la nature au cas général ?
Merci d'avance.