Page 1 sur 1
Suites.
Posté : mer. 10 sept. 2014 17:33
par Alice Term. S.
Bonjour,
Je bloque concernant une simplification:
Je ne vois pas trop comment continuer...
Merci d'avance.
Re: Suites.
Posté : mer. 10 sept. 2014 17:42
par SoS-Math(1)
Bonjour,
Pour le dénominateur de la fonction dérivée, vous pouvez écrire \(\left(\sqrt{x}\right)^2=x\).
Pour le numérateur, vous pouvez réduire au même dénominateur qui est \(2\sqrt{x}\).
Bon courage.
Re: Suites.
Posté : mer. 10 sept. 2014 21:31
par Alice Term. S.
Bonsoir,
Voici ce que j'ai fait mais je suis de nouveau bloquée:
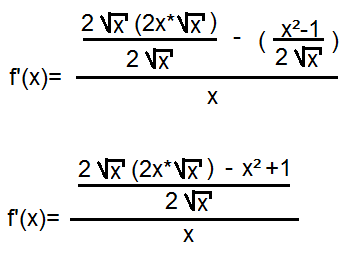
- Suites 2.png (4.69 Kio) Vu 4413 fois
Merci d'avance.
Re: Suites.
Posté : mer. 10 sept. 2014 21:36
par SoS-Math(1)
Bonsoir,
\(2x\sqrt{x}\times 2\sqrt{x}\) se simplifie.
De plus, \(\dfrac{\dfrac{a}{b}}{c}=\dfrac{a}{bc}\).
A bientôt.
Re: Suites.
Posté : dim. 14 sept. 2014 17:06
par Alice Term. S.
Bonjour,
Merci de votre réponse: cela donne:
f'(x)= (3x²+1)/2\(\sqrt{x}\)*x
Concernant le numérateur, j'ai un polynôme du 2nd degré. Mais comment puis-je étudier le signe de ma dérivée ?, le dénominateur pose problème.
Merci d'avance.
Re: Suites.
Posté : dim. 14 sept. 2014 20:42
par sos-math(13)
Bonjour Alice,
le dénominateur ne doit pas poser de problème : une racine carrée, on connaît son signe, et en plus, tu sais quel est le signe de x. Donc...
Bon courage.
Re: Suites.
Posté : dim. 14 sept. 2014 20:51
par Alice Term. S.
Bonsoir,
Merci de votre réponse:
La racine carrée est strictement positive sur R+ et x est négative sur moins l'infini 0 et positive sur 0 plus l'infini mais je suis bloquée concernant le tableau à faire, pour cette ligne, je ne vois pas comment faire.
Merci d'avance.
Re: Suites.
Posté : dim. 14 sept. 2014 21:27
par sos-math(13)
La racine carrée est strictement positive sur R+* (attention à l'étoile, pour le strictement) et ta fonction n'est définie que sur R+*, donc le signe de x est assez simple, non ?
Et le signe du produit aussi.
Re: Suites.
Posté : dim. 14 sept. 2014 22:19
par Alice Term. S.
Je n'avais pas fait attention à l'ensemble de définition.
Merci beaucoup.