Page 1 sur 1
Probabilités
Posté : lun. 9 juin 2014 14:31
par Melissa
Bonjour ! Je rencontre quelques difficultés à résoudre cet exercice.
" Deux cultivateurs A et B produisent respectivement 65% et 35% de la quantité totale de fraises vendues à une fabrique artisanale de confiture. Les pourcentages de fruits sains sont respectivement 97% et 95 %. On choisit une fraise au hasard. Si elle n'est pas saine, quelle est la probabilité pour qu'elle ait été cultivée par B ? "
J'ai fait un arbre pour m'aider :
97% sains
A 65%__ /_3% non sains
95% sains
B 35%__/_ 5% non sains
Mais finalement ça ne m'aide pas tant que ça pour résoudre ce problème, donc j'aurais besoin d'aide...
Merci d'avance :)
Re: Probabilités
Posté : lun. 9 juin 2014 14:45
par SoS-Math(9)
Bonjour Melissa,
Je ne comprends pas ton arbre ... voici le mien :
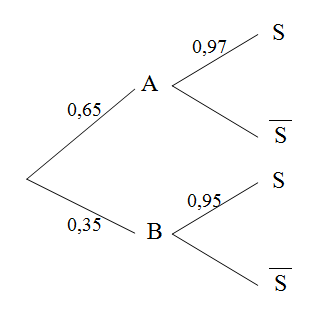
- arbre.PNG (4.72 Kio) Vu 1866 fois
Tu veux calculer \(P_{\overline{S}}(B)\) ... avec l'arbre ci-dessus cela doit être plus simple ...
SoSMath.
Re: Probabilités
Posté : lun. 9 juin 2014 14:48
par Mélissa
Je ne parvenais pas à faire un arbre correct ici mais c'est un comme le vôtre que je voulais reproduire en fait ! :)
Mais si on prend la formule P ( A si B ) = P ( A / B ) on prend quelles données ?! Je suis un peu perdue...
Re: Probabilités
Posté : lun. 9 juin 2014 15:06
par Mélissa
A représente 0.35 et le B on fait (65 % X 3 %) + (35 % X 5% ) = 0.037
Ce qui donne : 0.35 / 0.037 = 9.45
Est-ce correct ?
Re: Probabilités
Posté : lun. 9 juin 2014 15:11
par Mélissa
Je pense m'être trompée ! J'ai inversé A et B je pense...
La réponse est
0.037/0.35 = 0.10 donc 10 % de chance qu'elle ait été cultivée par B
Est-ce correct ?
Re: Probabilités
Posté : lun. 9 juin 2014 15:39
par SoS-Math(9)
Mélissa,
Quelle formule utilises-tu pour calculer \(P_{\overline{S}}(B)\) ?
ton calcul "(65 % X 3 %) + (35 % X 5% ) = 0.037 " représente \(P(\overline{S})\) ...
SoSMath.
Re: Probabilités
Posté : lun. 9 juin 2014 15:42
par Mélissa
La formule que j'utilise c'est
""Si B est un événement de probabilité non nulle, la probabilité que l'événement A se réalise, alors que l'événement B s'est déjà réalisé auparavant est donné par
P (A si B ) = P (A / B ) = P (A et B) / P (B) " ...
Re: Probabilités
Posté : lun. 9 juin 2014 15:47
par SoS-Math(9)
Mélissa,
c'est la bonne formule !
\(P(B\cap \overline{S})\) est donné par le chemin passant par B et \(\overline{S}\) ...
et \(P(\overline{S})\) est donné par la somme des probabilités des chemins menant à \(\overline{S}\).
SoSMath.
Re: Probabilités
Posté : lun. 9 juin 2014 17:01
par Mélissa
Donc on doit faire (0,05x0.35)/0,037 ce qui donne 0.47 donc 47% de chances
Re: Probabilités
Posté : lun. 9 juin 2014 18:19
par SoS-Math(9)
C'est bien Mélissa.
SoSMath.