Page 1 sur 1
produit scalaire
Posté : sam. 17 mai 2014 19:14
par Théo
Bonsoir
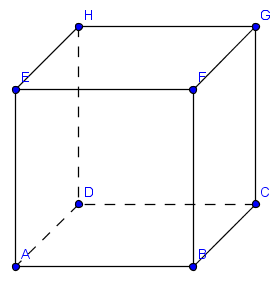
- cube.png (4.31 Kio) Vu 12542 fois
ABCDEFGH est un cube d'arrête 1.
Il faut que je démontre que DF.EG=0
Mais je n'arrive pas
Voilà ce que j'ai fait pouvez-vous me dire où est mon erreur svp
DF.EG=DF.AC=AF.AC=AB.AC
Merci de m'aider
Re: produit scalaire
Posté : dim. 18 mai 2014 13:18
par SoS-Math(9)
Bonjour Théo,
Tu as écrit : "DF.EG=DF.AC=AF.AC=..." c'est faux ... \(\vec{DF}\neq\vec{AF}\)
Par contre tu as \(\vec{DF}.\vec{AC}=(\vec{DB}+\vec{BF}).\vec{AC}=...\) avec cela tu dois pouvoir terminer.
SoSMath.
Re: produit scalaire
Posté : dim. 18 mai 2014 14:29
par Théo
Pourquoi c'est faux
Comment doit-on choisir le projeté orthogonal ?
Re: produit scalaire
Posté : dim. 18 mai 2014 15:10
par SoS-Math(9)
Théo,
Si tu veux utiliser les projetés orthogonaux, alors le projeté orthogonal de \(\vec{DF}\) est \(\vec{DB}\) (et non AF).
SoSMath.
Re: produit scalaire
Posté : dim. 18 mai 2014 15:20
par Théo
Pourquoi c'est DB et non AF ?
Re: produit scalaire
Posté : dim. 18 mai 2014 20:46
par sos-math(21)
Tout dépend sur quel plan tu projettes...
Si c'est sur le plan du bas, alors \(F\) se projette sur \(B\) donc mon collègue a raison.
Bon courage
Re: produit scalaire
Posté : dim. 18 mai 2014 21:07
par Théo
Désolé mais je ne comprends toujours pas pourquoi c'est c'est DB et non AF ?
Pourquoi D ne peut se projeter en A ?
Re: produit scalaire
Posté : lun. 19 mai 2014 06:42
par sos-math(21)
Quand on projette un point A sur un point plan (P), le projeté est le point B de ce plan tel que (AB) soit orthogonale au plan.
Donc tout dépend sur quel plan tu projettes.
Sur le plan du bas, D se projette sur lui-même : il fait partie du plan.
F se projette sur B, car (BF) est orthogonale au plan (ABCD).
Bonne continuation
Re: produit scalaire
Posté : lun. 19 mai 2014 06:52
par théo
Mais pourqioi DF ne peut pas être AF, pourtant A est le projeté orthogonal de D sur le plan ABEF ???
Re: produit scalaire
Posté : lun. 19 mai 2014 06:57
par sos-math(21)
Tu as raison pour la projeté sur le plan (ABEF) mais cela n'a aucun intérêt : il faut que tu projettes sur un plan contenant l'autre vecteur, ou un plan parallèle à celui-ci.
Bon courage
Re: produit scalaire
Posté : mar. 20 mai 2014 23:28
par Théo
Merci
Toujours avec la même figure
Ils demandent de calculer EC.BG est-ce que je peux écrire EC.BG=FC.BG=0 ??
Merci encore
Re: produit scalaire
Posté : mer. 21 mai 2014 14:28
par SoS-Math(4)
Bonjour,
oui , c'est juste , mais il faut expliquer.
Le mieux est d'utiliser la puissante relation de Chasles.
en vecteur:
EC.BG=(EF+FC).BG=EF.BG+FC.BG=0+FC.BG=FC.BG=0
sosmaths