Page 1 sur 2
Algorithme
Posté : dim. 3 nov. 2013 02:58
par Evans
Bonjour à tous.
J'ai un langage Algobox à faire et je trouve cela un peu compliquer, j'aurais besoin besoin d'un peu d'aide s'il vous plaît ^^"
Soit (Un) la suite définie par U1 = 3/2 et Un+1 = nUn+1/2(n+1)
Pour afficher la terme U9 de la suite (Un) un élève propos l'algorithme ci-contre. Il a oublié de compléter 2 lignes :
Variables n est un entier naturel
u est un réel
Initialisation Affecter à n la valeur
Affecter à u la valeur 1,5
Traitement Tant que n<9
Affecter à u la valeur ...........
Affecter à n la valeur ...........
FinTant que
Sortie Afficher la variable u
1. Compléter les 2 lignes manquantes
2. Comment faudrait-il modifier cet algorithme pour qu'il calcule et affiche tous les termes de la suite de U2 jusqu'à U9
3. Créer cet algorithme avec le language Algobox
4. Au vu des résultats, conjecturer le sens de variaton et la convergence de la suite (Un)
1. Pour les 2 lignes manquantes je pense que c'est Affecter à u la valeur 0 et Affecter à n la valeur uUn+1/2(u+1)
2. Tant que 2<n<9
3.
Re: Algorithme
Posté : dim. 3 nov. 2013 08:06
par sos-math(21)
Bonjour,
Dans ton algorithme, tu affectes 0 à la valeur u et il n'y a plus de modification de la variable u après, donc Algobox va t'afficher la valeur 0 pour u, ce qui est gênant car u est la variable qui va jouer le rôle de \(u_n\).
Donc il faudrait plutôt affecter à u l'expression qui définit \(u_{n+1}\) sauf qu'on ne peut pas mettre \(u_n\) dans l'expression (le logiciel ne le reconnaitra pas), il faut mettre u à la place, car c'est la variable qui joue le rôle de \(u_n\) dans ton algorithme.
Puis, pour que la boucle s'incrémente, c'est-à-dire passe d'un rang au suivant il faudra affecter à n la valeur ...
Bon courage
Re: Algorithme
Posté : dim. 3 nov. 2013 14:09
par Evans
Bonjour sos-math(21),
Donc sa voudrait dire que c'est :
1)Affecter à u la valeur nu+1/2(n+1) et Affecter à n la valeur 1
2) Tant que 2<n<9
Mais il y a quand même un problème la boucle s'arrête à la ligne 9...
Re: Algorithme
Posté : dim. 3 nov. 2013 15:10
par sos-math(21)
Mais c'est normal, on veut calculer \(u_9\),
c'est une boucle conditionnelle : tant que la valeur est inférieure à 9, on calcule le rang d'après, une fois que 9 est atteint on s'arrête.
Regardons ton algorithme :
- Pour l'affectation du u, c'est bon,
- mais si tu veux passer au rang suivant, il faut que n (qui joue le rôle de compteur) passe au rang suivant donc n prend la valeur ...
- Dans ton algorithme, le "lire u" est inutile..
Si on veut afficher tous les termes de la suite \(u_2,..., u_9\), il faut demander l'affichage de \(u\) à chaque calcul, donc à l'intérieur du "Tant que".
A toi de proposer un nouvel algorithme.
Est-ce plus clair ?
Re: Algorithme
Posté : dim. 3 nov. 2013 15:29
par Evans
alors,
1) Affecter à n la valeur u+1
2) A l'intérieur de tant que on va écrire :
Tant que 2<n<9
Affecter à u la valeur nu+1/2(n+1)
Affecter à n la valeur u+2
FinTant que
Re: Algorithme
Posté : dim. 3 nov. 2013 15:32
par sos-math(21)
Non, n est un nombre entier et u est un nombre réel, affecter à n la valeur "u+1" (ou "u+2") n'a aucun sens.
Quels compteur a-t-on dans une relation de récurrence ? Qu'est ce qui suit le rang n ?
Pour modifier l'algorithme afin d'afficher tous les termes de \(u_2\) à \(u_9\), il faut insérer une commande d'affichage mais à l'intérieur de la boucle, il y aura donc un affichage par tour.
Bon courage
Re: Algorithme
Posté : dim. 3 nov. 2013 15:50
par Evans
Ce qui suit le rang n dans une relation de récurrence c'est n+1
2) La commande d'affichage c'est dans Tant que ou après Fin tant que ?
Re: Algorithme
Posté : dim. 3 nov. 2013 15:57
par sos-math(21)
Donc on affecte à n la valeur n+1.
Si tu veux tous les termes de la suite, il faut demander l'affichage à l'intérieur de la boucle pour que celui-ci soit effectué à chaque tour.
Coche le saut de ligne dans la fenêtre "Affichage", ainsi, les termes seront écrits les un en dessous des autres.
Bon courage
Re: Algorithme
Posté : dim. 3 nov. 2013 18:48
par Evans
C'est bizarre mais dans mon affichage :
Barre d'outil
Cadre présentation
Changer police interface
Changer couleur console résultats
Mais il y a saut de ligne...
Re: Algorithme
Posté : dim. 3 nov. 2013 20:36
par sos-math(21)
Tu l'as fait tourner ?
Pour demander un retour à la ligne c'est au moment où tu choisis "Ajouter AFFICHER variable", la boite de dialogue suivante apparait et il faut cocher "Ajouter un retour à la ligne".
En revanche, avec cet algorithme, tu auras seulement la dernière valeur calculée \(u_9\), car l'affichage est en dehors de la boucle.
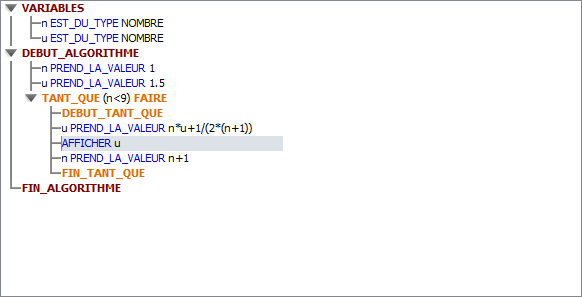
- algorithme_3_11_bis.png (11.19 Kio) Vu 7339 fois
Bon courage
Re: Algorithme
Posté : dim. 3 nov. 2013 21:31
par Evans
Merci pour ces explications supplémentaires.
Sa veut donc dire que pour le 2) il faudrait mettre 2<n<9 comme sa l'algorithme ne s'arrêtera plus qu'à 9 ? (Je suis un peu perdu pour le 2) :s )
Re: Algorithme
Posté : lun. 4 nov. 2013 07:55
par sos-math(21)
Oui, c'est cela.
Depuis le début, cet algorithme s'arrête à \(u_9\), c'est la condition n<9 du TANT QUE.
Re: Algorithme
Posté : mar. 5 nov. 2013 01:31
par Evans
Grâce à votre aide j'ai fais le 4) et j'ai dit que la suite est croissante et que la suite converge vers +infini. Mais j'ai comme un doute...
Re: Algorithme
Posté : mar. 5 nov. 2013 09:28
par sos-math(21)
Bonjour,
Juste une confirmation : la relation de récurrence est bien \(u_{n+1}=nu_n+\frac{1}{2(n+1)}\) ?
Tu as trouvé ta suite croissante et elle n'a pas l'air d'être majorée, donc elle a bien l'air de diverger vers \(+\infty\).
Bon courage pour la suite
Re: Algorithme
Posté : mar. 5 nov. 2013 22:16
par Evans
Bonjour, non la suite c'est le fichier ci-dessous :