Page 1 sur 2
Les suites
Posté : dim. 16 oct. 2011 22:24
par Mathilde
- Figure.png (5.62 Kio) Vu 3984 fois
Bonjour, pourriez-vous m'aider pour ceci ?
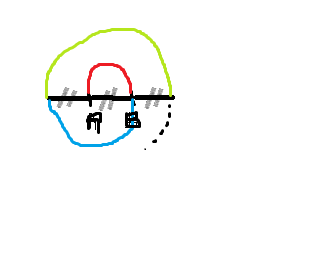
Une spirale
[AB] = 2cm
On construit à partir de ce segment une spirale formée de demi-cercles consécutifs comme ci-contre.
Soit Ln la longueur de la spirale formée de n demi-cercles (n>ou égal à 1)
1) Quel est le sens de variation de la suite ?
Croissante je pense
2) Déteminer L1, L2 et L3.
3) Exprimer Ln en fonction de n pour tout n>ou égal à 1.
4) Déterminer un indice n0 à partir duquel tous les termes Ln sont > à 1m.
5) La longueur de la spirale peut-elle dépasser 10km ?
Re: Les suites
Posté : lun. 17 oct. 2011 08:57
par sos-math(22)
Bonjour,
1) La suite semble effectivement croissante.
2) L1 est le périmètre d'un demi-cercle de diamètre 2 cm.
Le périmètre d'un cercle de diamètre D est \(\pi\times D\).
Donc \(L1=\frac{1}{2}\pi\times D=\frac{1}{2}\pi\times 2=\pi\).
As-toi maintenant de calculer L2.
Bonne continuation.
Re: Les suites
Posté : lun. 17 oct. 2011 14:59
par Mathilde
Bonjour ,
Ah d'accord ! Merci beacoup..
2)
Donc L2=1/2 π x D
L2=1/2 π x 4
L2= 2 π
L3=1/2 πxD C'est bien ça ?
L3=1/2 πx4
L3=3 π
3) Pour exprimer Ln en fonction de n :
Est-ce Ln=1/2 πxD ?
je ne comprends pas très bien..
4) et 5) Pourrai-je avoir une piste, ou autre, car je bloque totalement...
Re: Les suites
Posté : lun. 17 oct. 2011 15:24
par sos-math(22)
Regarde bien : L1=\(\pi\), L2=\(2\pi\), L3=\(3\pi\).
Ce n'est donc pas difficile de faire une conjecture.
Bonne continuation.
Re: Les suites
Posté : lun. 17 oct. 2011 15:35
par Mathilde
Ln = n π ?
Re: Les suites
Posté : lun. 17 oct. 2011 16:19
par sos-math(22)
Oui, c'est bien.
Re: Les suites
Posté : lun. 17 oct. 2011 16:31
par Mathilde
D'accord.
Pour la 4) et 5) , que dois-je faire ? ...
Re: Les suites
Posté : lun. 17 oct. 2011 16:38
par sos-math(22)
Merci de n'envoyer qu'un seul message. En envoyer plusieurs complique la gestion du forum.
Je te donne une indication de le 4) :
1 mètre correspond à combien de centimètres ?
Re: Les suites
Posté : lun. 17 oct. 2011 16:53
par Mathilde
Vous voulez dire de vous envoyer qu'une question par message ? ...
no=32 π ? (environ)
Re: Les suites
Posté : lun. 17 oct. 2011 17:23
par sos-math(22)
Oui de préférence, mais surtout de ne poster qu'un seul message à la fois, afin de ne pas faire de "doublon". \(32\pi\), oui, c'est bien cela mais essaye de bien distinguer valeur exacte et approchée et de bien préciser que \(n_0=32\) est la plus petite valeur de \(n\) entier naturel telle que l'on ait : \(n\pi>100\).
Re: Les suites
Posté : lun. 17 oct. 2011 20:00
par Mathilde
Ah oui pardon, ce n'était pas voulu, c''est car je croyais que je ne vous avez pas répondu, donc, j'ai envoyé 2fois...
D'accord merci beaucoup.
Avez-vous le temps pour m'aider sur un exercice de vecteurs ?
Re: Les suites
Posté : lun. 17 oct. 2011 20:13
par sos-math(21)
Bonsoir,
Cela dépend, si c'est juste une question, c'est jouable.
Re: Les suites
Posté : lun. 17 oct. 2011 20:20
par Mathilde
Une question oui, sur la colinarité...
Vecteurs : AE=2/3AJ
BF=2/3BC
Démontrer que I , E et D sont alignés.
Je n'arrive pas à démontrer que IE et ED sont colinéaires...
Re: Les suites
Posté : lun. 17 oct. 2011 20:23
par sos-math(21)
Quelle est la situation de départ ?
A, B, C sont placés comment ? Et ce point I, il est défini comment ?
Re: Les suites
Posté : lun. 17 oct. 2011 20:25
par Mathilde
Voici la figure
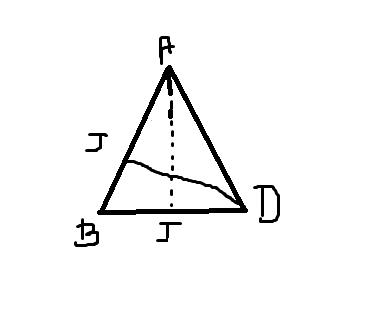
- Sans titre.png (5.59 Kio) Vu 3952 fois