Page 1 sur 1
Les Suites
Posté : mer. 5 mai 2010 15:46
par Charles
Bonjour j'ai un DM à faire il me reste quelques détails à régler.
Grand 2 questions 2 : j'ai tracé la courbe à partir de -1/2x+3
3)pour le sens de variation j'ai dit que (Un) ne semble pas être monotone sa suffit ? et quand on me demande de conjecturer la limite ( c'est 2) je dois dire que c'est divergent ou seulement à la fin ?
4b) exprimez Vn en fonction de n ....
Alors j'ai trouvé ) 4a que la raison r=-1/2 et de premier termes V0=-1
Vn=V0*q^n soit Vn= -1(-1/2)^n sa suffit pour exprimer Vn ?
les limites Vn q est compris entre -1 et 1 donc lim lorsque (Vn) tend vers +oo est 0
ensuite Un=Vn+2 donc sa limite c'est celle de Vn soit +2 donc lim lorsque n tend vers +00 = 2.
Pour le grand 3.
j'arrive pas à exprimez la fonction f telle que pour tout naturel n, Un+1=f(Un) ce qui me permettra de tracer la droite de la courbe. comme il l'est demandé à la question 2 du grand 2.
Merci
Re: Les Suites
Posté : mer. 5 mai 2010 16:18
par SoS-Math(4)
Bonjour Charles ,
3) C'est ça, mais une suite qui a une limite est convergente et non divergente. Donc cette suite U semble convergente puis que sa limite semble être 2.
4)b) bien
3) la fonction f est définie par \(f(x)=\frac{x-3}{x+1}\). Sa représentattion graphique n'est pas une droite .
sosmaths
Re: Les Suites
Posté : mer. 5 mai 2010 16:30
par Charles
Bonjour
il me manque plus qu'a prouvez la propriété de la question 2 du grand 3. par ou commencer s'il vous plaît.
Merci
Re: Les Suites
Posté : mer. 5 mai 2010 17:35
par SoS-Math(4)
Commence par calculer \(u_{n+3}\) en fonction de \(u_{n+2}\) en tenant compte de \(u_{n+3}=f(u_{n+2})\)
puis \(u_{n+2}\) en fonction de \(u_{n+1}\)
Utilise les formules obtenues pour montrer que \(u_{n+3}=u_n\)
sosmaths
Re: Les Suites
Posté : mer. 5 mai 2010 18:39
par Charles
Bonsoir j'ai remplacer Dans la fonction Un par U1 qui vaut -1/3 j'obtient Un+3= -5
Un+2 en fonction Un+1je sais pas
Mais c'est pas des formules que j'obtient donc c'est faux.
Merci
Re: Les Suites
Posté : mer. 5 mai 2010 20:25
par SoS-Math(4)
\(U_{n+3}=\frac{U_{n+2}-3}{U_{n+2}+1}\),
Remplacer dans cette expression \(U_{n+2}\) par \(\frac{U_{n+1}-3}{U_{n+1}+1}\)
Puis ensuite \(U_{n+1}\) par \(\frac{U_{n}-3}{U_{n}+1}\)
A la fin de tous les calculs( faites les ) on doit trouver \(U_{n+3}=U_{n}\)
sosmaths
Re: Les Suites
Posté : jeu. 6 mai 2010 14:48
par Charles
Bonjour donc j'ai fait les calculs mais j'ai pas de fin je me retrouve avec des calculs allant jusqu'a 4a5 barre de fraction en remplacer Un+2 par la totalité de l'expression avec Un+1-3/Un+1+1.
Merci
Re: Les Suites
Posté : ven. 7 mai 2010 07:11
par sos-math(19)
Bonjour Charles,
Après avoir remplacé \(u_{n+2}\) par son expression en fonction de \(u_{n+1}\),
tu simplifies la nouvelle expression obtenue pour \(u_{n+3}\)
et seulement, après cette première simplification, tu remplaces \(u_{n+1}\) par son expression en fonction de \(u_n\).
Tu simplifies cette nouvelle expression de \(u_{n+3}\) et tu dois obtenir le résultat annoncé.
Bonne continuation.
Re: Les Suites
Posté : ven. 7 mai 2010 18:37
par Charles
Bonjour j'obtient des Un élevée au carée je vous laisse vérifier la ou je me suis arrété car a mon avis je n'arrive pas a ce qui est demandé.
Merci
Re: Les Suites
Posté : ven. 7 mai 2010 22:30
par sos-math(19)
Bonsoir Charles,
A la ligne 2 (voir fichier joint L2.jpg), le remplacement serait correct. Encore faut-il faire attention aux niveaux d'écriture des indices des traits de fraction et du signe "=".
A la ligne 3 (voir fichier joint L3.jpg), de grosses erreurs de calcul.
Au numérateur tu devrais trouver : \(\frac{u_{n+1}-3-3u_{n+1}-3}{u_{n+1}+1}\).
Au dénominateur tu devrais avoir : \(\frac{u_{n+1}-3+u_{n+1}+1}{u_{n+1}+1}\).
Ce qui donne après simplification : \(\frac{u_{n+1}-3-3u_{n+1}-3}{u_{n+1}-3+u_{n+1}+1}\),
soit : \(\frac{-2u_{n+1}-6}{2u_{n+1}-2}\) que tu peux encore simplifier par 2 avant le remplacement de \(u_{n+1}\).
Essaye de continuer.
Sois plus rigoureux et respecte bien les règles opératoires.
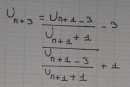
- L2.JPG (3.28 Kio) Vu 6611 fois

- L3.JPG (2.85 Kio) Vu 6611 fois
Re: Les Suites
Posté : dim. 9 mai 2010 17:20
par Charles
Bonsoir
après la simplifications par 2 et le calcul j'arrive à la fin sur -Un/Un-4 et non à Un comme il le faudrait.
Merci
je pense que je me trompe en replaçant au numérateur avec le moins devant le -Un-3 aprés simplification.
Re: Les Suites
Posté : dim. 9 mai 2010 21:08
par sos-math(19)
Bonsoir Charles,
Il te reste donc à calculer : \(\frac{-\frac{u_n-3}{u_{n}+1}-3}{\frac{u_n-3}{u_n+1}-1}\).
Bonne continuation.
Re: Les Suites
Posté : lun. 10 mai 2010 16:09
par Charles
Bonjour je ne trouve pas Un mais Un-6 cependant je pense savoir ou est mon erreur quand je met le numérateur - 3 sous le même dénominateur j'obtient -Un - 3 -3Un -3
-3-3 sa fait moins 6 et je pense que si la j'obtient -3+3 a la fin le calcul serait bon. donc le moins devant le trois me fait faire une érreur de signe.
En espérant avoir était clair désolé.
Merci.
Re: Les Suites
Posté : mar. 11 mai 2010 08:42
par sos-math(19)
Bonjour Charles,
Voici quelques erreurs à corriger, signalées dans des cercles rouges.
Figure N :
1. - le symbole d'égalité ne doit pas être utilisé ici, puisque le quotient n'est pas égal à son numérateur que tu calcules ici.
2. - Le symbole "moins" était devant le trait de fraction. Il commande tout le numérateur, donc si tu le montes sur le numérateur, tu dois changer simultanément les deux signes (exemple : l'opposé de (a+b) est (-a-b)).
3. - Ici, le signe "moins" est correct puisque tu as conservé ton signe "moins" devant le trait de fraction.
Figure D :
4. - Avec le signe "moins" le quotient que tu soustraits n'est pas égal à 1, comme il le devrait.
Essaye de corriger ces erreurs et soit plus attentif au niveau d'écriture des indices.
Bon courage

- Le numérateur de ta fraction.

- Le dénominateur de ta fraction.
- D.png (28.13 Kio) Vu 6596 fois