Page 1 sur 1
Exercice barycentre
Posté : ven. 19 févr. 2010 13:44
par Elise
Bonjour,
je sollicite votre aide pour un exercice de première S que j'ai vraiment beaucoup de mal a comprendre.
Celui-ci concerne les barycentres, voici l'énoncé :

- Enoncé de l'exercice
Ci dessous, j'ai essayer de répondre à la consigne de la partie A, mais je ne comprend pas trop l'énoncé... J'ai fait la figure avec (O;i), r=3...
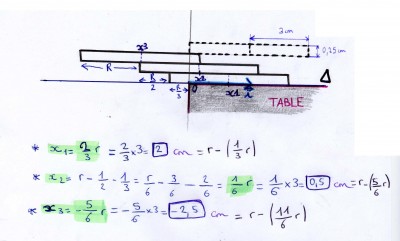
- Schéma
Puis j'ai calculé x1, x2 et x3 comme demandé, mais je ne sais pas du tout s'il fallait faire comme ça.
Et faut-il répondre à la première question "Montrez que le système est en équilibre, c'est à dire..." ou est-ce que l'on répond à la question au fur et à mesure des consignes? Enfin bref, pourriez-vous s'il vous plait m'éclairer.
Comme je n'avais pas compris l'exercice je ne me suis pas encore attaquée aux parties B), C) & D).
Merci beaucoup!
Re: Exercice barycentre
Posté : ven. 19 févr. 2010 22:32
par sos-math(19)
Bonsoir Elise,
Question A :
Attention à la numérotation des pièces.
\(x_1=r-(r+\frac{r}{2}+\frac{r}{3})\)
\(x_2=r-(\frac{r}{2}+\frac{r}{3})\)
\(x_3=r-(\frac{r}{3})\)
\(x_G=\frac{1}{3}(x_1+x_2+x_3)\)
Termine ce calcul.
Question B :
Il faut maintenant généraliser :
\(x_1=r-(...)\)
\(x_2=r-(...)\)
\(x_3=r-(...)\)
.
.
.
\(x_{n-1}=r-(...)\)
\(x_n=r-(...)\)
A toi de compléter à la place des pointillés.
Bon courage.
Re: Exercice barycentre
Posté : sam. 20 févr. 2010 15:33
par Elise
Bonjour,
tout d'abord merci pour votre aide.
Ci dessous voici le schéma avec la nouvelle numérotation des pièces, La pièce 1 est donc celle là plus haute:
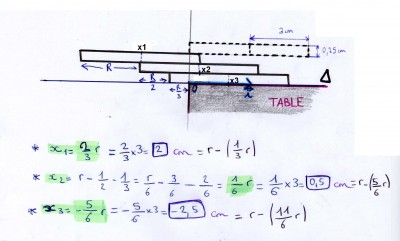
- Schéma avec correction
Pour la question A En vert, le début des calculs que vous m'aviez indiquez précédemant, je les ai ensuite dévelopés pour pouvoir répondre a la question suivante (avec xG):
x1 = r - (r + r/2 + r/3) = r - (11r/6)
x2 = r - (r/2 + r/3) = r - (5r/6)
x3 = r - (r/3) = r - (r/3)
J'ai donc pu conclure que :
xG = 1/3 ( x1 + x2 + x3)
= 1/3(r - 11r/6) + 1/3(r-5r/6) + 1/3(r-r/3)
= 1r/3 - 11r/18 + 1r/3 - 5r/18 + 1r/3 - 1r/9
=
0
Donc le centre d'inertir du solide constitué des 3 pièces se situe sur x=0, c'est donc bien à la verticale du bord de la table.
Je vais maintenant m'attaquer à la question B. J'espère que mes premiers résultats sont concluants.
Merci d'avance!
Re: Exercice barycentre
Posté : sam. 20 févr. 2010 16:23
par sos-math(19)
Bonjour Elise,
Les calculs \(x_1\), \(x_2\) et \(x_3\) sur le dessin ne correspondent pas à ceux du texte.
Les calculs corrects sont ceux du texte.
Ta conclusion est correcte.
Tu peux passer à la question B.
Dans cette question il ne faut pas chercher à réduire au même dénominateur le contenu de chaque paire de parenthèses.
Il faut simplement regrouper habilement les termes dans l'addition membre à membre.
Bonne continuation.
Re: Exercice barycentre
Posté : sam. 20 févr. 2010 17:09
par Elise
Oui, excusez-moi, les calculs sur le dessin pour la question A n'ont plus rien à voir, j'ai simplement oublié de les enlever...
Par contre pour la question B, malgré vos explications, je ne vois pas où il faut en venir...
Il faut maintenant généraliser :
x1 = r - (...)
x2 = r - (...)
x3 = r - (...) => pourquoi me demandez-vous de compléter ces trois calculs s'il faut généraliser à "n pièces"?
Je suis désolée mais je suis complètement perdue...
Merci
Re: Exercice barycentre
Posté : sam. 20 févr. 2010 19:49
par sos-math(19)
Bonsoir Elise,
Si tu veux bien jeter un coup d'œil à mon message du 19 à 22 h 32, il n'y a pas que 3 calculs à compléter.
Il y a une série de pointillés verticaux qui sous-entendent tous les calculs entre \(x_3\) et \(x_{n-1}\), et jusqu'à \(x_n\).
Pour comprendre la façon de généraliser, tu dois bien observer ce que tu as fait à la question A (3 pièces) :
x1 = r - (r + r/2 + r/3)
x2 = r - (r/2 + r/3)
x3 = r - (r/3)
J'espère que ces explications débloqueront la situation. Tu dois faire la même chose, mais avec \(n\) pièces.
Bonne continuation.
Re: Exercice barycentre
Posté : lun. 22 févr. 2010 15:20
par Elise
Bonjour,
malgré toutes vos explications, je ne vois toujours pas comment on peut généraliser à n pièces...
J'ai essayé de compléter le début de ce que vus m'aviez indiqué mais je ne suis vraiment pas sûre.
x1 = r - ( r + r/n-1 + r/n )
x2 = r - ( r/n-1 + r/n )
x3 = r - ( r/n )
Ce que j'ai fait me semble peu probable, car si l'on choisit n autre que 3 pièces, cela ne fonctionne plus.. Mais je ne vois pas comment généraliser à "n pièces" sinon...
J'espère que vous pourrez me donner une explication supplémentaire, je continue tout de même mes recherches..
Merci beaucoup!
Re: Exercice barycentre
Posté : lun. 22 févr. 2010 19:37
par sos-math(19)
Bonsoir Elise,
A titre d'exemple, et en espérant que le déclic s'opère, je te propose les formules pour 4 pièces :
\(x_1=r-(\frac{r}{1}+\frac{r}{2}+\frac{r}{3}+\frac{r}{4})\)
\(x_2=r-(\frac{r}{2}+\frac{r}{3}+\frac{r}{4})\)
\(x_3=r-(\frac{r}{3}+\frac{r}{4})\)
\(x_4=r-(\frac{r}{4})\)
On a alors : \(x_G=\frac{1}{4}(x_1+x_2+x_3+x_4)\)
Bonne continuation.
Re: Exercice barycentre
Posté : dim. 28 févr. 2010 10:14
par Elise
Bonjour,
Toujours bloquée à la partie B, je ne vois pas comment exprimer xn.
J'ai alors essayé d'exprimer xGn = 1/n ( n * x)
Merci
Re: Exercice barycentre
Posté : dim. 28 févr. 2010 15:40
par Elise
Re-bonjour,
En fait, c'est bon, j'ai réussi l'exercice. J'ai pu rencontrer un camarade qui m'a réexpliqué et j'ai enfin "tilté".
Navrée de vous avoir importuné, et merci pour toutes vos explications!
Bonne continuation!
Re: Exercice barycentre
Posté : mar. 2 mars 2010 10:05
par SoS-Math(7)
Il n'y a pas de problème, n'hésite pas à nous recontacter si tu as besoin.
Bonne journée