Page 1 sur 1
equation du second degré probleme
Posté : mar. 27 oct. 2009 17:52
par Marie
Bonjour à tous, J'ai un probleme avec un dm dont voici la premiere partie que je pense avoir reussie voici l'énoncé et mes réponses pouvez-vous me dire si c'est juste
On projette une diapositive sur un ecran à l'aide d'un projecteur.On peut modeliser ainsi ce diapositif (voir dessin)
pour regler la nettete de l'image de la diapositive sur l'ecran, on "regle l'objectif" ce qui revient a modifier la distance OA.
On montre que l'image est nette quand 1/OA+1/OA'=1/f , où f est une constante exprimée en metres, qui depend de l'objectif utilise.On prendra f=0.1m
On projette une diapositive sur un ecran à l'aide d'un projecteur.On peut modeliser ainsi ce diapositif (voir dessin)
. MISE EN EQUATION
On note D la distance AA' entre la diapositive et l'ecran , et d la distance OA pour laquelle l'image es nette.
1.Exprimer OA' en fonction de OA et de D.OA = d
OA' = D - d
f = 0,1
d'ou (1/d) + [1/(D-d)] = 1/0,1
d²-dD+0,1D=0
et si on remplace d par x, on obtient l'équation cherchée!!
2.En deduire que d est solution de l'equation (E): x²-Dx+0,1D=0.
3.Resoudre cette eqution pour D=3m et pour D=0.3m après avoir résolu l'équation du second degré je trouve pour D=3 ; x=(3-racine carrée de 7.8)/2
et x =(3+racine carrée de 7.8)/2
pour D=0.3m je trouve que le discriminant est négatif donc il n'y a pas de solutions Est-ce juste ?
3) en considerant le discrimanant de l'equation (E), montrer que l'ecran doit etre placé à au moins __cm de la diapositive pour obtenir une image nette. je trouve pour discriminant D(D-0.4) je sais que la conditions pour qu'un discriminant aient des racines réélle il doit etre nul ou supèrieur à 0 mais je ne sais comment conclure pour dire qu'il faut que d soit à 40 cm de l'écran
Merci de me dire si il ya des erreures car c'est très importants pour la suite que je ne comprends pas
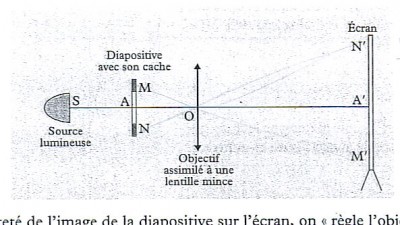
- voilà la figure
Re: equation du second degré probleme
Posté : mar. 27 oct. 2009 23:23
par SoS-Math(7)
Bonsoir Marie,
Ce que vous avez fait me semble bon.
3) vous savez que le discriminant vaut D(D-0,4) et vous savez que ce problème n'a de solution que si l'équation x²-Dx+0,1D=0 admet une solution. Il faut donc que le discriminant D(D-0,4) soit supérieur ou égal à zéro.
Je vous laisse réfléchir.
Re: equation du second degré probleme
Posté : mer. 28 oct. 2009 18:07
par marie 1ére S
Bonjour et merci de m'avoir répondu !
Pour le discriminant D(D-0.4) j'ai cherché et je ne sais pas si c'est juste mais voilà mon resonnement :
D est une distance d'ou D est supèrieur à 0
(D-0.4) supérieur ou egale à 0 pour D supèrieur ou égal à 0.4 car 0.4-0.4=0
Donc je remplace D par 0.4 dans 1/d+1/(D-d)=1/f avec f=0.1 (donné dans l'énoncé) cela nous donne (d+0.4-d)/(0.4d-d(au carré))=10 donc à la fin j'obtient 0.04=d(0.4-d) je sais que 0.04 m= 40cm mais je ne sais pas a quoi correspond d(0.4-d) pouvez vous m'éclaircir sachant que dans l'énoncé ils disent :montrer que l'ecran doit etre place à au moins 40cm de la diapoitive pour que l'on puisse obtenir une image nette.
Sinon je suis bloquée pour la suite du DM : Voilà l'enoncé
La diapositive [MN] a pour image sur l'ecran [M'N'] où M' et N' sont tels que M,O,M' soit alignes ainsi que N,O,N'.
(SA')est un axe de symetrie de la figure.
On pose y=taille de l'image sur l'ecran/taille de la diapositive =M'N'/MN
2.Montrer que y=OA'/OA . En deduire que y=(D/d)-1 pour cette question je pense utiliser thalès dans les triangles OAM et OA'M' ce qui nous donne OA/OA'=OM/OM' et ensuite dans les triangles OMN et OM'N' ce qui nous donne MN/M'N'=OM/OM' on peut conclure que OA'/OA=M'N'/MN=y Est- ce juste ?
4.b/ Si D>0,4m, montrer qu'il y a un unique reglage qui permet un agrandissement d l'image
Pour cette question je suis réellement bloquée pouvez vous me donner une piste ?
Merci infiniment de prendre le temps de vérifier mes reponses je vous en suis très reconnaissante.
Re: equation du second degré probleme
Posté : mer. 28 oct. 2009 22:41
par SoS-Math(7)
Bonsoir Marie,
Tu tournes un peu en rond... Tu veux que l'image puisse être nette donc d'après ce que tu as fait, elle le sera si l'équation (E): x²-Dx+0,1D=0 admet au moins une solution (la distance d pour que l'image soit nette). L'équation (E) admet au moins une solution si le discriminant est positif ou nul donc si D(D-0.4)>=0. Comme tu l'as dit D>=0 donc D(D-0.4)>=0 pour D-0,4>=0 et je pense que tu vas ainsi démontrer que l'image ne peut être nette que si l'écran est placé à au moins 40cm de la diapositive.
2) Ta proposition est tout à fait correct. L'égalité y=D/d -1 vient de la définition des longueurs OA' et OA.
4)b) Le réglage qui permet un agrandissement de l'image est la (ou les) longueur d tel que d soit solution de l'équation (E). Pour D>=0,4, ton équation (E) admet une ou deux solutions.
Le cas où D=0,4 est résolu, le discriminant étant nul, l'équation a une unique solution donc il existe un unique réglage.
Il ne te reste plus qu'à étudier le cas de figure où le discriminant est strictement positif et donc l'équation admet 2 solutions distinctes. Petite indication, d est la longueur OA, c'est donc un nombre positif !
Bonne recherche.
Re: equation du second degré probleme
Posté : jeu. 29 oct. 2009 17:53
par marie 1ére S
Bonsoir,
Je suis vraiment très embêtée car je ne sais plus du tout comment faire pour trouver la question 3 qui est :en considerant le discriminant de l'equation (E), montrer que l'ecran doit etre placé à au moins 40 cm de la diapositive pour obtenir une image nette. je trouve pour discriminant D(D-0.4).
Déja je sais que la distance entre l'écran et la diapositive est notée D donc je cherche à montrer que D=40cm soit 0.04m jusque là je pense que tout est bon mais admettons que D=0.04m alors le discriminant est négatif car 0.04(0.04-0.4)infèrieur à 0 or j'ai démontrer que D>=0 donc D(D-0.4)>=0 pour D-0,4>=0 d'ou D=0.4 pour que le discriminant soit nul il admet donc une seule solution d=-b/2a pour que l'image soit nette or moi je dois trouver la distance entre l'écran et la diapositive (soit D) pour que l'image soit nette donc il ne faut pas que je calcule d.
Mais comment trouver D=0.04m avec D(D-0.4) sachant que je ne comprend même pas comment cela est-ce possible pour que D=0.04m alors que le discriminant est nul pour D=0.4; je suis donc perdue deboussolée.
ensuite pour la dernière question :
Quand D=0.4 je sais que l'image n'est pas aggrandie.y=1
Quand D supèrieur à 0.4 le discriminant est strictement positif l'équation admet 2 solutions distinctes comme d est la longueur OA, et que c'est un nombre positif on a comme unique solution d=(D+racine carrée de (D(D-0.4))/2 est-ce cela l'unique réglage qui permet l'agrandissement de l'image ?
Ce que je ne comprend pas c'est pourquoi on utilise le discriminant de l'équation permettant la netteté de l'image alors que dans cette question il est question de l'agrandissement de l'image ou l'equation déjà demontrée est (D/d)-1 donc je pense qu'il ne faut pas utiliser le discriminant de la netteté de l'image pour Si D>0,4m, montrer qu'il y a un unique reglage qui permet un agrandissement d l'image.
Voilà mes recherches pas très fructueuses car je suis encore plus perdues qu'avant. Si vous pouviez encore un peu plus me guider ce serait formidable car j'ai beau tourner le probleme dans tout les sens je ne vois pas comment faire.
Merci.
Re: equation du second degré probleme
Posté : jeu. 29 oct. 2009 21:52
par SoS-Math(7)
Bonsoir Marie,
Tu sembles avoir perdu le fil du problème. Reprends les indications données :
Tu veux que l'image puisse être nette donc d'après ce que tu as fait, elle le sera si l'équation (E): x²-Dx+0,1D=0 admet au moins une solution (la distance d pour que l'image soit nette).
L'équation (E) admet au moins une solution si le discriminant est positif ou nul donc si D(D-0.4)>=0.
Comme tu l'as dit D>=0 donc D(D-0.4)>=0 pour D-0,4>=0 et je pense que tu vas ainsi démontrer que l'image ne peut être nette que si l'écran est placé à au moins 40cm de la diapositive.
Tu as bien compris la suite de l'exercice. Le réglage de la netteté de l'image est bien l'une des solutions de ton équation (E) et il est donc normal que le discriminant soit encore là. Par contre, tu sembles penser que d2=(D-racine carrée de (D(D-0.4))/2 est un nombre négatif, or c'est un nombre positif...
En effet, racine carrée de (D(D-0.4))<D
Il faut donc trouver une autre justification pour qu'une seule des deux racines soit acceptable et c'est là que l'agrandissement rentre en jeu...
Je te propose de regarder de plus près le résultat de (D/d)-1 pour d= (D-racine carrée de (D(D-0.4))/2
J'espère t'avoir rassurée et remise sur la problématique de ton exercice.
Bon courage
Re: equation du second degré probleme
Posté : ven. 30 oct. 2009 17:51
par marie 1ére S
Bonsoir après de longues reflexions j'arrive à cette démarche :
Pour la question :montrer que l'ecran doit etre placé à au moins 40 cm de la diapositive pour obtenir une image nette, le discriminant D(D-0.4) est nul pour pour D=0.4 donc il faut que D soit supèrieur ou égal à 0.4m soit 40cm pour que l'image soit nette c'est juste cela la justification à cette question ?
Ensuite pour la question 4 lorsque D supèrieur à 0.4 alors le discriminant est supèrieur à 0 donc il y a deux solutions distinctes pour l'équation (E): x²-Dx+0,1D=0 ou x=d
Calcul de d=(D-(racine carrée de (D(D-0.4)))/2 ou d=(D+(racine carrée de(D(D-0.4)))/2
Je sais que l'image est aggrandie lorsque d infèrieur à 1/2 de D et lorsque (D/d)-1 supèrieur à 1 donc je remplace d par (D-(racine carrée de (D(D-0.4)))/2 puis par (D+(racine carrée de(D(D-0.4)))/2 dans (D/d)-1 et je trouve
(D/d)-1 superieur à 1
(D/(D-(racine carrée de (D(D-0.4)))/2) supèrieur à 2
D supèrieur à 2((1/2)D-(racine carrée de D(D-0.4)/2)
D supèrieur à D-D(D-0.4) donc on a bien d infèrieur à 1/2 de D car (1/2)D supèrieur à (D-(racine carrée de (D(D-0.4)))/2
par conséquent il existe un unique réglage permettant un agrandissement de l'image pour d=(D-(racine carrée de (D(D-0.4)))/2
Avant que je montre que avec d=(D+(racine carrée de(D(D-0.4)))/2 cela n'est pas possible pouvez vous me dire si déjà mon parcours est juste et si je dois traduire l'expression d=(D-(racine carrée de (D(D-0.4)))/2 par une distance plus expressive ?
Merci encore pour votre aide qui m'est précieuse.
Re: equation du second degré probleme
Posté : lun. 2 nov. 2009 14:37
par SoS-Math(7)
Bonjour Marie,
L'explication pour la distance de la diapositive à l'écran est correcte.
Pour l'agrandissement, il n'y a pas deux conditions mais soit l'une, soit l'autre, elles sont liées. Je te propose de comparer D/d-1 à 1.
Pour cela écris le calcul (D/d-1), mets le tout sous le même dénominateur et compare le numérateur et le dénominateur pour conclure.
Premier cas : \(\frac{D}{\frac{D-\sqrt{\Delta}}{2}}-1=\frac{2D}{D-\sqrt{\Delta}}-1=...\)
Je te laisse finir.
Re: equation du second degré probleme
Posté : ven. 6 nov. 2009 10:34
par mARIE
Bonjour et merci de m'avoir répondu !
Visiblement j'étais sur une mauvaise piste même si mes calculs me paraissaient juste car à la fin je trouvais que l'unique réglage permettant un agrandissement de l'image est lorsque la distance d=( D-(racine carrée de (D-(D-0.4)))/2 m
Avec votre aide je trouve quand je remplace dans (D/d-1), d par ( D-(racine carrée de (D-(D-0.4)))/2 je trouve :
(3D-(racine carrée du discriminant))/D-(racine carré du discriminant) comme (3D-(racine carrée du discriminant)) supérieur à D-(racine carré du discriminant) alors (3D-(racine carrée du discriminant))/D-(racine carré du discriminant) supérieur à 1 donc l'image est agrandie pour d=( D-(racine carrée de (D-(D-0.4)))/2 m
. Est-cela ? Est-ce que je dois montrer que pour d=(D+(racine carrée de (D-(D-0.4))/2 il n'y a pas d'agrandissement ?
Merci pour votre aide, j'espère arriver à la fin du problème !
Re: equation du second degré probleme
Posté : lun. 9 nov. 2009 23:45
par SoS-Math(7)
Bonsoir Marie,
Oui, votre raisonnement me semble juste, il faut montrer que pour l'autre racine, le résultat est inférieur à 1.
A bientôt
Re: equation du second degré probleme
Posté : mer. 11 nov. 2009 15:43
par Els4
Bonjour !
Moi aussi j'ai cet exercice en DM de maths, et tout comme toi j'avais certaines difficultés ! Pour la partie A, à mon goût j'ai tout réussi, mais, je bloque sur la partie B !
J'ai réussi à prouver qu'il fallait le placé à au moins 40cm en faisant donc une inéquation. Puis, j'ai fait aussi Thalès pour trouver la question 2). Par contre, je ne comprends pas la question 4) a) qui dit : Montrer que l'image sur l'écran est agrandie si et seulement si d<1/2D.
Merci de bien vouloir m'aider :) !
Re: equation du second degré probleme
Posté : ven. 13 nov. 2009 18:14
par SoS-Math(9)
Bonsoir Els4,
Pour avoir des éléments de réponse pour la question 4a), relit les messages postés.
SoSMath.
Re: equation du second degré probleme
Posté : dim. 17 oct. 2010 16:25
par sa
Bonjour, j'ai aussi ce devoir en maths. Je précise que je l'ai fait entièrement seul. Je bloque cependant a la 4. b)
Apres avoir relu plusieurs fois vos explications, je ne ois toujours pas l'explication quant au réglage que l'on doit faire pour obtenir une image agrandie
Re: equation du second degré probleme
Posté : dim. 17 oct. 2010 20:11
par SoS-Math(7)
Bonsoir,
Pour la 4 b), il y a deux parties :
rechercher les distances d qui permettent d'obtenir une image nette. On a vu (relire ce qui a été fait avant) que ces deux distances \(d_1\) et \(d_2\) étaient les racines de l'équation (E): x²-Dx+0,1D=0.
Ensuite, il faut regarder si ces deux position de "netteté" constituent un agrandissement de l'image.
Je sais que l'image est agrandie lorsque d inférieur à 1/2 de D donc lorsque (D/d)-1 supérieur à 1
En effet, \(d<\frac{D}{2}\) équivaut à (d positif) \(\frac{D}{d}>2\) soit \(\frac{D}{d}-1>1\)
Il faut comparer \(\frac{D}{d}-1\) à 1 pour les deux distances \(d_1=\frac{D+\sqrt{D(D-0,4)}}{2}\) et \(d_2=\frac{D-\sqrt{D(D-0,4)}}{2}\)
Bonne continuation.