SOS-MATH

Bonjour, je ne comprend pas cet exercice
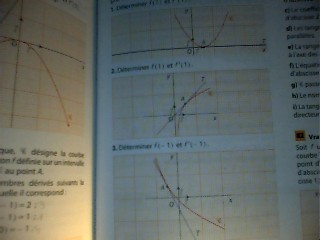
Dans chaque graphique, C désigne la courbe représentative d'une fonction f définie sur un intervalle et T désigne la tangente à C au point A
pour le graphique 1 et 2 déterminer f(1) et f '(1)
pour le graphique 3 déterminer f(-1) et f '(-1)

Bonjour,

Il s'agit donc d'une lecture graphique.
Pour le graphique 1 :

Pour déterminer f(1), il faut chercher sur la courbe représentative de f, le point qui a pour abscisse 1.
Alors f(1) est l'ordonnée de ce point.
Pour déterminer f ' (1), il faut chercher sur la courbe représentative de f le point qui a pour abscisse 1, le même que précédemment. En ce point la courbe admet une tangente. Alors f '(1) est le coefficient directeur de cette tangente.
Il semble ( car je lis pas bien sur vos figures) que cette tangente soit parallèle à l'axe des abscisses donc que son coefficient directeur soit 0. Donc f ' (1)=0.

Pour les autres figure la méthode est exactement la même. La difficulté que vous pouvez avoir , c'est de lire le coefficient directeur des tangentes. Regardez alors dans votre livre , c'est certainement expliqué quelque part.

Bon courage
sosmaths

pour le 1er graphique c'est f(1)=0 et f '(1)=0
pour le 2eme c'est f(1)=1
pour le 3eme c'est f(-1)=1
mais pour f ' j'ai du mal

Bonsoir,

Pour lire la valeur de f'(1), il faut déterminer le coefficient directeur de la tangente en A. Vous avez deux possibilité :
1- Vous vous placez sur un point de la tangente, vous vous déplacez de 1 unité vers la droite et vous lisez la valeur du déplacement vertical nécessaire pour rejoindre un point de la tangente. Si votre déplacement est vers le bas, le coefficient est négatif, si le déplacement est vers le haut, il est positif.
2- Vous pouvez calculer ce coefficient en déterminant les coordonnées de deux points de la droite et en utilisant la formule suivante : \(a=\frac{y_B-y_A}{x_B-x_A}\) où \(a\) est le coefficient.

Bon courage et à bientôt

Bonjour,
pour le 1er graphique c'est f(1)=0 et f '(1)=0
pour le 2eme c'est f(1)=1 et f '(1)=2
pour le 3eme c'est f(-1)=1 et f '(-1)=-2

voila est ce que tous ces résultats sont bons ?

Bonsoir,
1) les deux nombres sont justes
2) le nombre dérivé est faux
3) les deux nombres sont justes.
Bon courage pour revoir le 2)

pour le 2eme c'est f(1)=1 et f '(1)=1

Bonsoir,

C'est bon.

à bientôt sur sos-math.