Page 1 sur 1
Vecteur exo7)
Posté : sam. 27 janv. 2018 06:02
par Antony
Bonsoir,
Alors pour le numéro 7) a) je rencontre des difficultés je ne vois pas où est l’angle delta et comment le trouver.
Si vous voyez mal premier recteur norme de u =109 et l’orien 37 degré, deuxième rectangle norme de v=84 et l’orien 106 degré et troisième carré norme de w=126 et l’orien270 degré.
Merci de votre aide.
Re: Vecteur exo7)
Posté : sam. 27 janv. 2018 12:26
par SoS-Math(25)
Bonjour Antony,
Tu as déjà calculé les coordonnées de chaque vecteur. Il suffit ensuite de calculer les coordonnées du vecteur demandé. Par exemple :
Pour trouver l'abscisse du vecteur \(\vec{u}+\vec{v}\), on additionne les abscisses des vecteurs \(\vec{u}\) et \(\vec{v}\).
De même pour les ordonnées.
Bon courage !
Re: Vecteur exo7)
Posté : sam. 27 janv. 2018 14:04
par Antony
Vous pas bien lu l’an question c’est écrit Dans chaque cas déterminé la norme et l’orientation du vecteur résultant.
C’est pour cela qu’a L’aide de mon dessin je vous demande comment calculer l’angle Delta puisque je le vois dans le corrigé comme réponse il y a la Rome et l’orientation.Merci de votre aide.
Re: Vecteur exo7)
Posté : sam. 27 janv. 2018 14:14
par Antony
Par exemple pour le a) le corrigé arrive à (159,69 ,66,41 degré)
Re: Vecteur exo7)
Posté : sam. 27 janv. 2018 15:19
par SoS-Math(9)
Bonjour Antony,
voici un graphique pour visualiser les angles :
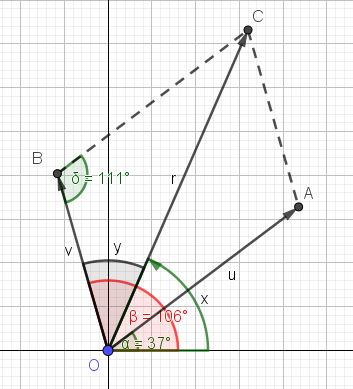
- Anglesvecteurs.JPG (38.26 Kio) Vu 2857 fois
Dans le triangle OBC on a : \(\frac{sin(y)}{109} = \frac{sin(111)}{159,69}\) ce qui va te donner \(y\).
Ensuite l'orientation de r sera donné par x ... où x+y = 106°.
SoSMath.