Page 1 sur 3
Ryan
Posté : mer. 22 nov. 2017 17:20
par Maximale, minimale
Bonsoir,
J'ai un exercice à faire pour demain, et j'ai passé presque 1 heure à chercher et j'ai fait ce que j'ai pus.
A tout point M du segment [AB], on associe les triangles équilatéraux AMP et MBQ.
1. Déterminer M pour que l'aire du triangle MPQ soit maximale.
2. Déterminer M pour que l'aire du quadrilatère ABQP soit minimale.
(On pourra choisir x= distance AM )
1. on pose AM = x et MB = 1 - x comme les triangles AMP et MBQ sont equilateraux donc les côtés ont même mesure .
Je voudrais essayer d'utiliser le théorème de Pythagore pour calculer la hauteur des deux triangles.
Pour la 2. je ne vois pas comment faire. J'ai des idées mais je ne sais pas comment les mettre en pratique.
Merci d'avance pour votre aide.
Re: Ryan
Posté : mer. 22 nov. 2017 18:21
par SoS-Math(33)
Bonsoir,
ton idée d'utiliser le théorème de Pythagore pour calculer la hauteur des triangles est bonne.
Utilise le schéma ci-dessous pour t'aider dans les calculs.
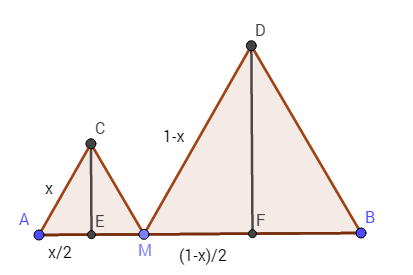
- geogebra-export.png (10.8 Kio) Vu 9931 fois
Je te laisse commencer cette question
Re: Minimal, maximal
Posté : mer. 22 nov. 2017 19:22
par Ryan
Selon Pythagore, dans un triangle rectangle abc, c étant l'hypoténuse on a l'équation suivante : a^2 + b^2 = c^2
Pour le triangle APM : Pour le triangle MBQ :
( 1-x/2 )^2 + b^2 = ( 1-x)^2 x^2 +b^2 = ( x/2 )^2
b^2 = ( 1 + x^2/4 ) + ( 1 + x^2 ) b^2 = x^2 + ( x^2/4 )
b^2 = ( 1 + x^2/4 ) + ( 4 + 4x^2 /4 ) b^2 = ( x^2/4 ) +( x^2/4 )
b^2 = 5 + 5x^2 /4 b^2 = 2x^2 /4
La hauteur du triangle AMP mesure 5 + 5x^2/4
La hauteur du triangle MBQ mesure 2x^2 /4
Est-ce correct ?
Re: Ryan
Posté : mer. 22 nov. 2017 19:31
par SoS-Math(33)
Ce que tu écris est un peu confus.
Tes résultats ne sont pas corrects, il ne peut pas y avoir de x² dans tes hauteurs.
Dans le triangle AMC:
AC²=AE²+CE² remplaces par les valeurs et calcules CE
Dans le triangle MDB:
MD²=MF²+FD² remplaces par les valeurs et calcules FD
A toi de faire les calculs
Re: Minimal, maximal
Posté : mer. 22 nov. 2017 19:56
par Ryan
AC^2 = AE^2 + CE^2 MD^2 = MF^2 + FD^2
x^2 = ( x/2 )^2 + CE^2 ( 1 - x )^2 = ( 1 - x/2 )^2
CE^2 = x^2/4 - x^2 FD^2 = ( 1 + x^2/4 ) - ( 1 + x^2 )
CE = V( 2x^2/4 ) FD = V( 1 + x^2/4 ) - V( 1 + x^2 )
CE = x/2 FD = ( 1 + x/2 ) - ( 1 + x )
FD = 1 + x - 2 + 2x /2
FD = -1 + 3x/2
Re: Minimal, maximal
Posté : mer. 22 nov. 2017 20:08
par Ryan
Mon message a mal été pris, je le reposte différemment. Si vous voulez.
Re: Ryan
Posté : mer. 22 nov. 2017 20:09
par SoS-Math(33)
Tes calculs sont incorrects.
Fais attention à ton écriture car comme tu peux le voir ci-dessous ce que tu écris n'est pas affiché comme tu le souhaites et c'est très confus à suivre.
Ryan a écrit :AC^2 = AE^2 + CE^2 MD^2 = MF^2 + FD^2
x^2 = ( x/2 )^2 + CE^2 ( 1 - x )^2 = ( 1 - x/2 )^2
CE^2 = x^2/4 - x^2 FD^2 = ( 1 + x^2/4 ) - ( 1 + x^2 )
CE = V( 2x^2/4 ) FD = V( 1 + x^2/4 ) - V( 1 + x^2 )
CE = x/2 FD = ( 1 + x/2 ) - ( 1 + x )
FD = 1 + x - 2 + 2x /2
FD = -1 + 3x/2
\(x^2 = ( x/2 )^2 + CE^2\)
\(CE^2 =\)
-\(x^2/4\)
+ \(x^2\)
\(CE^2=3x²/4\)
\(CE=\frac{\sqrt{3}}{2} x\)
A toi de reprendre tes calculs pour le second triangle
Re: Minimal, maximal
Posté : mer. 22 nov. 2017 20:28
par Ryan
( 1 - x ) ^2 = ( 1 - x/2)^2 + FD^2
FD^2 = ( -1 + x^2 /4 ) + ( 1 - x^2 )
FD = V( -1 + x^2 /4 ) + V( 1 - x^2 )
FD = ( -1 + x /2 ) + ( 1 - x )
FD = -1 + x + 2 - 2x /2
FD = 1 - x /2
Re: Ryan
Posté : mer. 22 nov. 2017 20:37
par SoS-Math(33)
Attention :
\(MF = \large\frac{1-x}{2}\) donc \(MF^2 = \large\frac{(1-x)^2}{4}\)
\(MD = (1-x)\) donc \(MD^2 = (1-x)^2\)
Reprends le calcul MD²=MF²+FD²
Re: Minimal, maximal
Posté : mer. 22 nov. 2017 21:01
par Ryan
MD^2 = MF^2 + FD^2
( 1 - x )^2 = ( 1 - x )^2 /4 + FD^2
FD^2 = ( -1 + x )^2 /4 + ( 1 - x )^2
FD = V( -1 + x )^2 /4 + V( 1 - x )^2
FD = ( -1 + x )/2 + ( 1 - x )
On met au même dénominateur non ?
Je crois avoir fait la même erreur mais je ne vois pas où.
Re: Ryan
Posté : mer. 22 nov. 2017 21:09
par SoS-Math(33)
Ryan a écrit :MD^2 = MF^2 + FD^2
( 1 - x )^2 = ( 1 - x )^2 /4 + FD^2
FD^2 = ( -1 + x )^2 /4 + ( 1 - x )^2 c'est FD^2 = -( 1 + x )^2 /4 + ( 1 - x )^2
FD = V( -1 + x )^2 /4 + V( 1 - x )^2
FD = ( -1 + x )/2 + ( 1 - x )
On met au même dénominateur non ?
Je crois avoir fait la même erreur mais je ne vois pas où.
Il y a beaucoup d'erreurs dans ta réponse.
Tu n'as pas le droit de passer de \(a^2 = b^2+c^2\) à \(a = \sqrt{a^2} + \sqrt{b^2}\) c'est \(a = \sqrt{b^2+c^2}\)
Il faut reprendre tes calculs.
Re: Minimal, maximal
Posté : mer. 22 nov. 2017 21:37
par Ryan
FD^2 = -( 1 + x )^2 /4 + ( 1 - x )^2
FD = -V( 1 + x )^2 /4 + V( 1 - x )^2
FD = -1 - x + 4 - 4x /4
FD = 3 - 5x /4
Re: Ryan
Posté : mer. 22 nov. 2017 21:40
par SoS-Math(33)
Prends le temps de relire le message précédent pour corriger tes erreurs.
Re: Minimal, maximal
Posté : mer. 22 nov. 2017 21:49
par Ryan
FD^2 = -( 1 + x )^2 /4 + ( 1 - x )^2
FD = V-( 1+x)^2 /4 + ( 1-x )^2
FD = -( 1 + x )/2 + ( 1 - x )
FD = -1 - x + 2 - 2x /2
FD = -x + 1 /2
Re: Ryan
Posté : mer. 22 nov. 2017 22:01
par SoS-Math(33)
C'est toujours pas ça.
Je pense que tu devrais faire une pause et reprendre l'exercice demain à tête reposée.
\(-\large\frac{(1-x)^2}{4} \normalsize + (1-x)^2\) dans cette expression factorise \((1-x)^2\) avant de prendre la racine carrée
Bonne soirée
SoS-math