Page 1 sur 1
un cylindre inscrit dans une sphère
Posté : sam. 28 mars 2015 19:46
par Clary
Bonjour à vous,
J'ai un petit problème avec un exercice sur les sphères.
Voici l'énoncé :
Pour aménager un parc, on dispose de sphères de rayon 6 dm. À l'intérieur on veut placer des poubelles de forme cylindrique. On suppose qu'une poubelle a pour hauteur 2h et pour rayon r (en dm). On cherche à déterminer la hauteur du cylindre pour obtenir une poubelle de volume maximal.
1. a) Exprimer r en fonction de h.
b) Démontrer que le volume V du cylindre en dm3 peut s'écrire sous la forme V (h)=2(pi)(-h(au cube)+36h)
2. a) Déterminer la hauteur du cylindre pour laquelle le volume de la poubelle est maximal.
b) Déterminer la valeur exacte de ce volume en dm3.
c) Donner l'arrondi à l'unité de ce volume.
Je n'arrive pas à r en fonction de h. Je pense que une fois ça fait le reste ira tout seul.
Merci d'avance de votre aide,
Bonne journée.
Re: un cylindre inscrit dans une sphère
Posté : sam. 28 mars 2015 20:01
par SoS-Math(9)
Bonsoir Clary
Pour la question 1 : tu as un triangle rectangle JID, qui te donne 6²=h²+r². Voir figure ci-dessous :
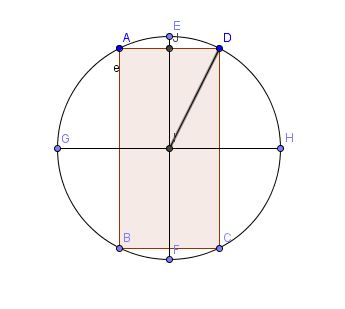
- Sphère.JPG (16.04 Kio) Vu 13315 fois
SoSMath.
Re: un cylindre inscrit dans une sphère
Posté : sam. 28 mars 2015 20:39
par Clary
Merci de votre réponse.
J'ai utilisé le théorème de Pythagore et je suis arrivé à : r=racine carrée de(6(au carré)-h(au carré)
Est ce que c'est juste ?
[Je suis désolé, mais je ne pas faire les racines et les carrés]
Re: un cylindre inscrit dans une sphère
Posté : sam. 28 mars 2015 20:47
par SoS-Math(9)
C'est bien Clary.
SoSMath.
Re: un cylindre inscrit dans une sphère
Posté : sam. 28 mars 2015 21:19
par Clary
Pour la question 2-a, il y a faut résoudre une équation à deux inconnues ?
Re: un cylindre inscrit dans une sphère
Posté : sam. 28 mars 2015 21:26
par SoS-Math(9)
Bonsoir Clary,
Pour la question 2a, tu as une seule inconnue x ...
Il faut étudier les variations de V(x) ... pour cela dérive ta fonction V(x), puis étudie son signe.
SoSMath.
Re: un cylindre inscrit dans une sphère
Posté : dim. 29 mars 2015 00:31
par Clary
Merci de votre aide.
Re: un cylindre inscrit dans une sphère
Posté : dim. 29 mars 2015 09:14
par SoS-Math(9)
A bientôt,
SoSMath.
Re: un cylindre inscrit dans une sphère
Posté : mar. 5 mai 2015 12:40
par Lili
Bonjour, j'ai reçu le même exercice . Mon seul problème est dans la question n°1 ou je dois exprimer r^2 en fonction de h .
J'ai donc utilisé le triangle ABC et j'ai appliqué Pythagore et j'ai trouvé :
AC^2= AB^2 + BC^2
12^2 = 2h^2 +r^2
Je voudrais savoir si ce raisonnement était le bon.
Merci de votre aide.
Re: un cylindre inscrit dans une sphère
Posté : mar. 5 mai 2015 13:07
par SoS-Math(9)
Bonjour Lili,
il y a deux erreurs :
il manque les parenthèses et BC = 2r et non r (BC est le diamètre de la base du cylindre).
D'où
12^2 = (2h)^2 +(2r)^2
SoSMath.
Re: un cylindre inscrit dans une sphère
Posté : mar. 5 mai 2015 13:21
par Lili
Merci de votre réponse. En refaisant la question j'ai trouver en résultat final :
r^2= h^2- 36
Est-ce le bon résultat ?
Merci de votre aide.
Re: un cylindre inscrit dans une sphère
Posté : mer. 6 mai 2015 10:32
par SoS-Math(9)
Bonjour Lili,
C'est le bon résultat.
SoSMath.
Re: un cylindre inscrit dans une sphère
Posté : ven. 15 févr. 2019 16:06
par Manon
Bonjour,
J'ai un problème pour la question 1-b.
Je ne comprend pas d'où viens le 2π...
Merci de votre aide !
Re: un cylindre inscrit dans une sphère
Posté : sam. 16 févr. 2019 08:44
par SoS-Math(33)
Bonjour,
le volume d'un cylindre est : aire de la base x hauteur.
La base étant un disque de rayon R l'aire de cette base est \(\pi\) R²
Il te faut trouver le rayon du cylindre et sa hauteur.
SoS-math