Page 1 sur 2
Dm non fini
Posté : jeu. 8 mai 2014 16:23
par Charlie

- Screenshot_3.jpg (17.36 Kio) Vu 4290 fois
Je refais un sujet car on ne repond plus, c'est pour demain svp aider moi j'y arrive vraiment pas.
J'ai réussi le 1)
le reste je n'y parviens pas...
u=racine de x
u'=1/2racine de x
v=x+1
v'=1.
1
___ *(x+1) - √x*1
2√x
______________________
(x+1)²
Re: Dm non fini
Posté : jeu. 8 mai 2014 19:02
par SoS-Math(1)
Bonsoir,
Le calcul de la fonction dérivée est bon.
Il faut maintenant transformer cette écriture en multipliant le numérateur et le dénominateur par \(2\sqrt{x}\).
Bon courage.
Re: Dm non fini
Posté : jeu. 8 mai 2014 19:41
par Charlie
1
___ *(x+1) - √x*1
2√x
______________________
(x+1)²
donc:
1
___ *(x+1) - √x*1 *2√x
2√x
______________________
(x+1)² * 2√x
=
x+1 - √x
______________________
(x+1)² * 2√x
Que dois-je faire ensuite svp?
Re: Dm non fini
Posté : jeu. 8 mai 2014 20:49
par SoS-Math(1)
Bonjour,
Attention au numérateur, vous avez \((x+1)-2\sqrt{x}\times \sqrt{x}=x+1-2x\) car \(\sqrt{x}^2=x\).
A bientôt.
Re: Dm non fini
Posté : jeu. 8 mai 2014 20:57
par Charlie
donc au numerateur on trouve 1-x mais au dénominateur le 2√x c'est annuler non?
Re: Dm non fini
Posté : jeu. 8 mai 2014 21:01
par SoS-Math(1)
Bonsoir,
Non, au dénominateur on trouve \(2\sqrt{x}(x+1)^2\).
D'ailleurs, c'est ce qu'il faut trouver d'après votre énoncé.
A bientôt.
Re: Dm non fini
Posté : jeu. 8 mai 2014 21:17
par Charlie
bah comment on a "supprimer" le 1/2√x ? dans le numerateur
Re: Dm non fini
Posté : jeu. 8 mai 2014 22:16
par SoS-Math(1)
Bonsoir,
Si vous multipliez \(\dfrac{1}{2\sqrt{x}\) par \(2\sqrt{x}\), cela fait 1.
A bientôt.
Re: Dm non fini
Posté : ven. 9 mai 2014 06:39
par Charlie
Bonjour
Pour le multiplier, cela veux dire que le 2racx du numérateur c'est supprimer?
Re: Dm non fini
Posté : ven. 9 mai 2014 21:10
par sos-math(21)
Bonsoir,
on a \(f'(x)=\frac{\frac{1}{2\sqrt{x}}\times (x+1)-\sqrt{x}}{(x+1)^2}\) et en multipliant par \(2\sqrt{x}\) au numérateur ET au dénominateur, on a :
\(f'(x)=\frac{\left(\frac{1}{2\sqrt{x}}\times (x+1)-\sqrt{x}\right)\times 2\sqrt{x}}{(x+1)^2\times 2\sqrt{x}}\) soit en développant au numérateur, on a
\(f'(x)=\frac{x+1-2x}{\2\sqrt{x}\times(x+1)^2}\) : je te laisse terminer....
Bonne continuation
Re: Dm non fini
Posté : sam. 10 mai 2014 09:52
par Charlie
Ok je l'ai fini merci.
Maintenant je bloquer au 3) j'ai réussi a faire le tableau mais pas la suite...
Re: Dm non fini
Posté : sam. 10 mai 2014 10:10
par SoS-Math(9)
Bonjour Charlie,
Le tableau de variations de f te donne le minimum et le maximum de f sur [0 ; +inf[.
Donc tu as l'encadrement : pour tout x de [0 ; +inf[, min de f =< f(x) =< max de f.
SoSMath.
Re: Dm non fini
Posté : sam. 10 mai 2014 12:06
par Charlie
Bonjour,
Je n'ai pas saisi votre dernier message... pouvez-vous me réexpliquer
Re: Dm non fini
Posté : sam. 10 mai 2014 12:55
par SoS-Math(9)
Charlie,
Le tableau de variations d'une fonction te permet d'avoir (s'ils existent) le minimum et le maximum d'une fonction sur son intervalle de définition.
Voici un exemple :
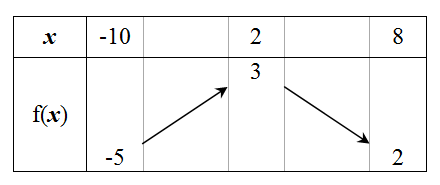
- Tab_Var.PNG (4.49 Kio) Vu 4259 fois
Ici pour tout x de [-10 ; 8], le minimum de f est -5 et le maximum est 3.
Donc pour tout x de [-10 ; 8], -5 =< f(x) =< 3.
SoSMath.
Re: Dm non fini
Posté : dim. 11 mai 2014 18:34
par Charlie
Bonjour,
ok merci,
J'ai essayé le 4 et 5 mais je n'y arrive pas pouvez-vous m'aider?