Page 1 sur 7
devoir maison
Posté : lun. 21 avr. 2014 21:57
par marie berthonneau
Bonjour,
comment peut-on resoudre une inequation graphiquement ?
Merci
Re: devoir maison
Posté : mar. 22 avr. 2014 07:00
par sos-math(21)
Bonjour,
Cela dépend de ton inéquation.
S'il faut résoudre \(f(x)\geq \alpha\), alors il faut tracer la droite horizontale d'équation \(y=\alpha\) et voir les portions de la courbe représentative de f situées au-dessus de cette droite.
Il reste ensuite à lire les abscisses correspondantes, cela te donnera les solutions.
Je t'envoie un exemple de résolution graphique : \(f(x)\geq 2,5\) :
Précise ta question si tu veux que notre réponse soit plus précise.
Bonne continuation
Re: devoir maison
Posté : mar. 22 avr. 2014 18:05
par marie berthonneau
La courbe (|-) ci contre represente une fonction f definie sur R et deux de ses tangentes
La premiere question est la suivante :
1)a l'aide du graphique repondre aux questions suivantes :
A)resoudre l'inequation f(x)>0
B)resoudre l'inequation f'(x)>0))
C)determiner f'(0)
D)doner une equation de la tangente a (|-)en B
la deuxieme question est la suivante :
2)on sait maintenant que f(x)=6x+6/x au carre +3
A)retrouver la reponse a la question 1)a)
B)calculer f'(x) et retrouver la reponse a la question 1 b)
La troisieme question est la suivante :
3)on cherche a savoir s'il y a une tangente a (|-) passant par l'origine O du repere. Soit A d'abscisse a un point de (|-)
A)determiner l'equation de la tangente a la courbe e
b)montrer que la tangente en A a (|-) passe par O si et seulement si f(a)=a * f'(a)
c)montrer que l'equation ci-dessus est equivalente a 2a au cube + 3a au carre +3 =0
d)en vous aidant de votre calculatrice, determinez le nombre de solutions de cette equation. Expliquer.
Re: devoir maison
Posté : mer. 23 avr. 2014 07:28
par sos-math(21)
Bonjour,
Il ne s'agit pas d'envoyer tout l'énoncé d'un bloc mais plutot de nous dire à quel endroit tu as bloqué.
Je te donne le début : résoudre \(f(x)>0\) revient à déterminer pour quelles abscisses, la courbe est au-dessus de l'axe des abscisses.
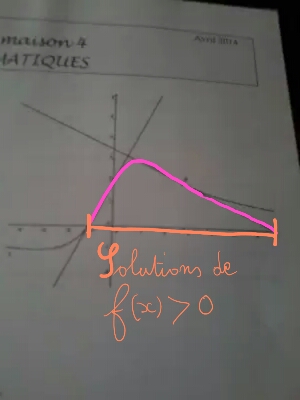
- 2014-04-23 08.23.23.jpg (51.93 Kio) Vu 3366 fois
Pour \(f'(x)>0\), cela revient à chercher sur quel intervalle la dérivée de f est strictement positive, ce qui signifie f strictement croissante.
Fais déjà cela et précise ce que tu ne comprends pas dans un nouveau message.
Bon courage
Re: devoir maiso n
Posté : mer. 23 avr. 2014 07:36
par marie berthonneau
comment trouver la derivee ?
Re: devoir maison
Posté : mer. 23 avr. 2014 07:50
par sos-math(21)
Il ne s'agit pas de trouver la dérivée, tu ne peux pas la trouver.
Il s'agit d'utiliser le lien entre une fonction et sa dérivée : la dérivée est positive sur les intervalles où la fonction est croissante ;
la dérivée est négative sur les intervalles où la fonction est décroissante.
Ici tu veux \(f'(x)>0\) donc il s'agit de regarder sur quels intervalles ta fonction est (strictement) croissante.
Bonne lecture de graphique.
Re: devoir maison
Posté : mer. 23 avr. 2014 08:28
par marie berthonneau
Ensuite pour determiner f'(0) on fait comment ?
Re: devoir maison
Posté : mer. 23 avr. 2014 10:25
par sos-math(21)
Tu as du voir que la dérivée pouvait aussi s'interpréter graphiquement avec la notion de tangente : f'(0) est le coefficient directeur de ta tangente au point de la courbe d'abscisse 0. Celle-ci est tracée, il te reste à repérer sur cette tangente deux points A et B dont les coordonnées sont faciles à lire et à utiliser la formule permettant de calculer le coefficient directeur : \(f'(0)=m=\frac{y_B-y_A}{x_B-x_A}\).
Bon calcul
Re: devoir maison
Posté : mer. 23 avr. 2014 10:41
par marie berthonneau
Je comprends pas trop
Re: devoir maison
Posté : mer. 23 avr. 2014 10:58
par marie berthonneau
Ensuite je suis a la question 1)d) vous pouvez m'aider ?
Re: devoir maison
Posté : mer. 23 avr. 2014 11:45
par SoS-Math(7)
Bonjour,
La tangente est tracée, il faut donc lire l'ordonnée à l'origine (c'est à dire la valeur de l'ordonnée du point d'intersection de la tangente avec l'axe des ordonnées) et, avec la même méthode que pour le calcul d'avant, déterminer le coefficient directeur de la droite. Tu auras alors les valeurs de \(a\) et de \(b\) pour l'équation réduite qui est \(y=ax+b\).
Bon courage.
Re: devoir maison
Posté : jeu. 24 avr. 2014 15:45
par marie berthonneau
Donc si on reprend pour la question a ne trouve f(x)>0 sur l'intervalle -1 ; 7
la question b je trouve f'(x)>0 revient a trouver sur quelle intervalle la derivee de f est striictement croissante soit - infini ; 1
la question c je trouve f'(0)= 2
la question d jai pris deux points A (1 ; 3) et B (3;2) ensuite j'ai utiliser la formule YB-YA / XB-XA soit 2-3/3-1 egal a -1/2
est-ce que toutes ces reponses de la question 1 sont justes. Je peux passer a la question 2 ?
Re: devoir maison
Posté : jeu. 24 avr. 2014 17:29
par sos-math(21)
Pour la question d, on te demande l'équation complète donc il faut trouver le \(p\) tel que \(y=\frac{-1}{2}x+p\).
Complète ta réponse.
Re: devoir maison
Posté : jeu. 24 avr. 2014 17:42
par marie berthonneau
Comment on trouve le p? Sinon les autres reponses sont justes ?
Re: devoir maison
Posté : jeu. 24 avr. 2014 18:00
par sos-math(21)
Ta droite passe par A(1 ; 3) donc les coordonnées de A vérifient cette équation,
autrement dit quand on remplace \(x\) par 1 et \(y\) par 3, on a une équation d'inconnue \(p\) : ce sont des notions de seconde ....
Pour le reste, c'est bon à part que tu as dit :
revient a trouver sur quelle intervalle la derivee de f est striictement croissante soit - infini ; 1
: ce n'est pas la dérivée qui est strictement croissante mais la fonction.
Bon courage