Page 1 sur 1
Inéquations
Posté : jeu. 10 mars 2011 21:10
par Tipaza
Bonjour, je souhaiterais savoir comment résoudre :
Il me faudrait juste finir la factorisation et trouver les racines, mais je ne voit vraiment pas comment faire.
3
________ > ou = à x - 3
x² - x - 1
J'ai déjà fait :
[ 3 - ( x-3 ) ( x² - x - 1 ) ]
______________________ > ou = à 0
x² - x - 1
qui me donne : - x au cube + 4x² - 2x
____________________ > ou = à 0
x² - x - 1
Je dois aussi résoudre cette inéquation à l'aide d'un tableau de signe, mais je pourrais me débrouiller. Je vous remercie d'avance.
Re: Inéquations
Posté : ven. 11 mars 2011 07:59
par sos-math(20)
Bonjour,
En factorisant x au numérateur vous obtiendrez : \(\frac{x(-x^2+4x-2)}{x^2-x-1}\).
Il ne vous restera plus qu'à étudier le signe de chacun des facteurs dans un tableau de signe pour connaître le signe du quotient.
Bon courage.
SOS-math
Re: Inéquations
Posté : ven. 29 avr. 2011 13:40
par Bagheera
Bonjour, j'ai un petit soucis. Je ne sais pas trop comment fonctionne se site mais merci de bien vouloir m'aider.
Cela fait une semaine que je me tue à essayer mon devoir maison.
L'énoncé: Résoudre les inéquations suivantes et représenter l'ensemble des solutions graphiquement sur une droite graduée.
a) -3x-(4+x)strictement supérieur ou égale à 3x
c) 2-4xstrictement supérieur ou égale à -5x.
(j'ai pas pus écrire le b de l'énoncé parce qu'il y'a une fractions mais c'est rien. & désolé des "strictement supérieur ou egale à" mais mon ordi fait pas les signes mathématiques.)
Je vous demande juste de m'aider pour la partie " Représenter l'ensemble des solutions graphiquement sur une droite graduée."
MERCI D'AVANCE.
_ Bagheera!
Re: Inéquations
Posté : ven. 29 avr. 2011 16:39
par SoS-Math(7)
Bonjour,
Pour représenter l'ensemble des solutions par une droite graduée, il faut avoir résolu l'inéquation proposée. Lorsque vous aurez une solution du type \(x<\frac{-2}{3}\), il faut alors utiliser une droite graduée sur laquelle vous placez \(\frac{-2}{3}\).
Ensuite, par convention, on hachure la partie de la droite où se situent les nombres non solution de l'inéquation. Au niveau de la valeur \(\frac{-2}{3}\), il faut mettre un crochet que l'on oriente soit vers l'ensemble des solutions (dans le cas d'une inéquation large : inférieur ou égal à, supérieur ou égal à) soit dans l'autre sens dans le cas d'une inégalité stricte (comme ici).
Dans cet exemple, cela donne :
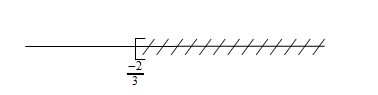
- Sos_math.PNG (2.25 Kio) Vu 1359 fois
Bonne continuation.