Page 1 sur 2
Démontrer que MA + MB = 2 MI
Posté : dim. 14 janv. 2018 12:12
par léo
Bonjour
étant donné un segment [AB]
Pour tout point M du plan MA + MB = 2 MI
démonstration
je ne vois pas comment placer le point M pour cette démonstration
Pouvez vous m'aidez ? s'il vous plait
Re: Démontrer que MA + MB = 2 MI
Posté : dim. 14 janv. 2018 12:16
par SoS-Math(33)
Bonjour Léo,
comment est défini le point I, est-ce le milieu de [AB]?
Re: Démontrer que MA + MB = 2 MI
Posté : dim. 14 janv. 2018 12:19
par léo
Bonjour Sos math 33
merci de me répondre si vite !!
je bloque sur cette démonstration depuis deux semaines....
Re: Démontrer que MA + MB = 2 MI
Posté : dim. 14 janv. 2018 12:29
par léo
on va avoir trois points
les points A et B du segment [AB]
le point I
et le point M
Re: Démontrer que MA + MB = 2 MI
Posté : dim. 14 janv. 2018 12:31
par SoS-Math(33)
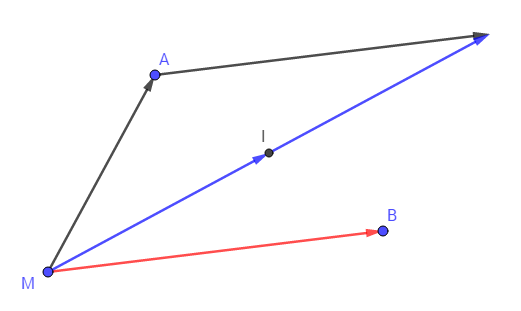
- geogebra-export.png (8.42 Kio) Vu 13422 fois
Cette propriété est valable pour n'importe quel point M du plan.
\(\overrightarrow{MA} + \overrightarrow{MB} = \overrightarrow{MI} + \overrightarrow{IA} + \overrightarrow{MI} + \overrightarrow{IB}\)
\(= 2\overrightarrow{MI} + \overrightarrow{IA} + \overrightarrow{IB}\)
\(=2\overrightarrow{MI}\) car \(\overrightarrow{IA} + \overrightarrow{IB} = \overrightarrow{0}\) I étant milieu de [AB]
Re: Démontrer que MA + MB = 2 MI
Posté : dim. 14 janv. 2018 12:40
par léo
au collège, nous avons qu'en traçant la médiatrice d'un segment [AB] on avait AM = MB
c'est à dire une égalité de longueurs -- > c'est bien cela ?
Re: Démontrer que MA + MB = 2 MI
Posté : dim. 14 janv. 2018 12:42
par SoS-Math(33)
Oui c'est bien cela.
Mais la question de ton sujet est pour des vecteurs ou des longueurs?
Re: Démontrer que MA + MB = 2 MI
Posté : dim. 14 janv. 2018 12:43
par léo
le point M peut être n'importe où sur la médiatrice
Re: Démontrer que MA + MB = 2 MI
Posté : dim. 14 janv. 2018 12:45
par SoS-Math(33)
Léo la question que tu pose à savoir MA + MB = 2MI est ce pour des longueurs ou pour des vecteurs?
Re: Démontrer que MA + MB = 2 MI
Posté : dim. 14 janv. 2018 12:52
par léo
la sujet porte sur les vecteurs pas sur les longueurs
Re: Démontrer que MA + MB = 2 MI
Posté : dim. 14 janv. 2018 12:54
par SoS-Math(33)
Si c'est les vecteurs alors le point I est le milieu de [AB] ou est -il hors du segment [AB]?
Re: Démontrer que MA + MB = 2 MI
Posté : dim. 14 janv. 2018 13:06
par léo
tout ce que j'ai compris en cours c'est :
\(\overrightarrow{AI}=\overrightarrow{IB}\Leftrightarrow\) I milieu du segment [AB]
-
Re: Démontrer que MA + MB = 2 MI
Posté : dim. 14 janv. 2018 13:10
par SoS-Math(33)
Il te faut relire la réponse que j'ai donné plus haut avec le schéma :
Re: Démontrer que MA + MB = 2 MI
Posté : dim. 14 janv. 2018 13:14
par léo
sur le schéma que vous avez fait : on voit que les points A, I et B sont alignés
Re: Démontrer que MA + MB = 2 MI
Posté : dim. 14 janv. 2018 13:16
par SoS-Math(33)
Bin oui puisque I est le milieu de [AB] sinon c'est pas possible