SOS-MATH

Bonjour SOS math

Pouvez vous m'expliquez pourquoi on dit que :

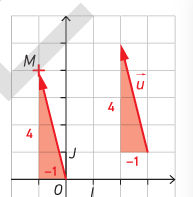
Les coordonnées de M sont (-1;4)

donc celles de \(\overrightarrow{u}\) sont \(\begin{pmatrix} -1\\4 \end{pmatrix}\)

Bonjour Nico,

Par définition, si M a pour coordonnées (1 ; 4), alors \(\vec{OM}\) a pour coordonnées (1 ; 4).
Comme \(\vec{OM}=\vec{u}\) (même direction, même sens et même longueur), donc ils ont les mêmes coordonnées. D'où \(\vec{u}\)(1 ; 4).

SoSMath.

Bonjour

Dans le dessin, L'origine du vecteur \(\overrightarrow{OM}\) est l'origine du repère, c'est à dire 0
mais si je place \(\overrightarrow{OM}\) en partant d'un autre point, est ce que je peux dire que les coordonnées du point M sont les mêmes que celles du vecteur \(\overrightarrow{u}\)

Bonjour,
les coordonnées d'un vecteurs et celle d'une des extrémités d'un de ses représentants sont identiques dans le seul cas où l'origine du vecteur est placée à l'origine du repère : cela tient à la définition des coordonnées d'un vecteur \(\left(\begin{array}{c}x_{\overrightarrow{AB}}\\y_{\overrightarrow{AB}}\end{array}\right)=\left(\begin{array}{c}x_B-x_A\\y_B-y_A\end{array}\right)\) donc on égalité \(\left(\begin{array}{c}x_{\overrightarrow{AB}}\\y_{\overrightarrow{AB}}\end{array}\right)=\left(\begin{array}{c}x_B\\y_B\end{array}\right)\) seulement quand \(x_A=0\) et \(y_A=0\) donc quand \(A=O\).
Bonne continuation

Super !

Merci SOS math