Page 1 sur 1
Fonction polynome du second degré
Posté : jeu. 27 avr. 2017 22:36
par Henri
Bonsoir,
J'ai commencé à effectuer l'exercice ci-dessous pour m'entrainer à ce chapitre des fonctions polynômes que je trouve un peu compliqué mais je bloque dès la première question, pouvez vous me donner quelques pistes, je n'arrive vraiment pas
Voici la consigne et les questions :
La puissance délivrée par une pile qui débite un courant d'intensité i dans un circuit est donnée par :
P(i)= 1,2i-0,4i² (P est exprimé en watts et i en ampères). La pile ne fonctionne que lorsque P(i)>0.
1) Montrer que l'intensité doit vérifier 0<i<3.
2)On appelle C la courbe représentative de P.
a) Quel est l'axe de symétrie de C
b) Donner le tableau de variations de P.
3) Pour quelle valeur de l'intensité la puissance délivrée est-elle maximale ? Calculer cette puissance maximale
4) Tracez la courbe C
Je vous remercie enormément de votre réponse, j'en ai besoin
Re: Fonction polynome du second degré
Posté : ven. 28 avr. 2017 08:55
par SoS-Math(9)
Bonjour Henri,
La puissance n'est définie que si elle est positive. Donc il faut résoudre l'inéquation : P(i) > 0.
Pour cela il faut factoriser P(i) puis faire un tableau de signes ...
SoSMath.
Re: Fonction polynome du second degré
Posté : ven. 28 avr. 2017 11:17
par Henri
Bonjour j'ai compris,
Il faut donc factoriser :
i( 1,2 -0,4 i) > 0
soit i > 0
et soit
i = 1,2-0,4 i > 0
-0,4 i < - 1,2
i < 3
Est-ce correct ?
c'est tout ou suis-je obligé de réaliser le tableau de signe ? Je ne comprend pas à quoi il peut servir
Merci de votre aide
Re: Fonction polynome du second degré
Posté : ven. 28 avr. 2017 12:47
par Henri
Bonjour les solutions sont alors
0 < i
et
i > 3
c'est juste ?
Je ne comprend pas comment faire le tableau de signes , je suis perdu et je ne comprend pas en quoi cela peut me servir
Re: Fonction polynome du second degré
Posté : ven. 28 avr. 2017 14:06
par SoS-Math(30)
Bonjour Henri,
Le tableau de signes est très pratique pour obtenir le signe d'un produit ou d'un quotient de fonctions affines car avec le tableau on est sûr de traiter tous les cas possibles.
Dans ton exercice, tu t'es seulement dit que pour que le produit soit positif il suffit que chaque facteur soit positif. Tu oublies alors de traiter le cas où les deux facteurs sont négatifs ce qui donne alors aussi un produit positif. Il se trouve qu'ici ce n'est pas possible d'avoir les deux facteurs négatifs en même temps mais tu ne l'as pas justifié.
Le plus simple est donc de construire le tableau de signes du produit et de lire ensuite pour quelles valeurs le produit est-il strictement positif.
Pour construire le tableau de signes, tu dois identifier les valeurs qui annulent chaque facteur : ici, 0 et 3.
Tu les ordonnes dans la première ligne de ton tableau qui représente les valeurs possibles de la variable i.
Puis tu écris une ligne pour le signe de i et une autre ligne pour le signe de 1,2-0 4 i
Enfin une quatrième ligne pour déterminer le signe du produit i(1,2 - 0,4 i) que tu obtiens en appliquant la règle des signes "colonne par colonne".
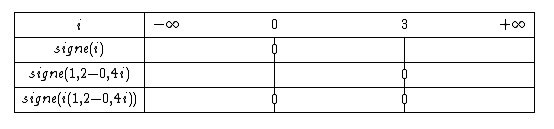
- tab_signe.png (3.59 Kio) Vu 4846 fois
Je te laisse compléter.
SoSMath
Re: Fonction polynome du second degré
Posté : ven. 28 avr. 2017 15:23
par Henri
Bonjour,
J'ai fait la première question, voici ma réponse, pouvez vous me dire si mes calculs sont corrects et enlever le doute dont je vous ai fait déjà part dans les deux messages précédents :
Il faiut résoudre l'inequation :
P(i) > 0 :
i (1,2-0,4i) > 0
Soit i>0
Et 1,2-0,4i>0
-0,4i> -1,2
i < -1,2 / -0,4
i < 1,2 / 0,4
i < 3
EST-CE CORRECT ?????
Puis tableau de signe :
Signe i (première ligne en horizontal) : - puis + et +
Signe 1,2-0,4i (deuxième ligne en horizontal ) : + et + puis -
Signe i (1,2-0,4i) (troisième ligne en horizontal) : - puis + puis -
Donc i (1,2-0,4i) > (ou égal) 0 sur [0;3]
Et i (1,2-0,4i) < (ou égal) 0 sur ]-infini;0] U [3;+infini[
On veut P>0, donc il nous faudra absolument la condition 0<i<3
EST-CE JUSTE ?
Merci beaucoup de votre aide
Re: Fonction polynome du second degré
Posté : ven. 28 avr. 2017 16:05
par SoS-Math(9)
C'est très bien Henri.
SoSMath.
Re: Fonction polynome du second degré
Posté : ven. 28 avr. 2017 18:09
par Henri
Merci beaucoup !
Re: Fonction polynome du second degré
Posté : ven. 28 avr. 2017 19:26
par SoS-Math(30)
A bientôt sur SoSMath