SOS-MATH

Bonjour, alors voilà j'ai un dm à faire pour jeudi prochain et je suis totalement perdue voici l'énoncé si joint. Si quelqu'un pourrait m'aider sa serait super.

Bonsoir Ambre,
Le principe de ce forum n'est pas de faire les exercices à ta place. Tu dois les commencer et après, je pourrai t'aider là où tu bloques. Pour calculer des volumes, tu dois utiliser des formules...
Bon courage et à bientôt.
Sos-math.

Bonjour Ambre,
pour l'exercice 1, il te faut calculer le volume de la cuve en décomposant : volume pyramide + volume cube
Rappel volume pyramide \((Aire de la base \times hauteur)/3\)
Tu vas obtenir un volume en \(cm^3\)
Ensuite tu convertis les 17500L en \(cm^3\) pour voir si le niveau de l'eau est dans la partie pyramide ou dans la partie cube.
Je te laisse faire les calculs.

pour l'exercice 2, tu peux essayer de voir quel solide on peut ajouter à la piscine pour obtenir une pavé droit.

alors j'ai fait 2,5X2,5 = 6,25m3 qui est l'aire du carré après j'ai calculée le volume du carré 2,5 au cube = 15,62m3
et après le volume de la pyramide 6,25X3/3 =6,25m3 et la je pense qu'il faut les additioner donc 6,25+15,62 =21,87m3 mais la j'ai un problème je pense que je dois soustraire 6,25 car avec le volume de la pyramide et du carré un côté est comme calculé deux fois (la base de la pyramide) mais je suis pas sur.
après j'ai convertis les L en cm3 et sa me donne 17500=1750000cm3 et la je comprend pas trop comment on peu savoir ou se trouve le niveau de l'eau.

Bonjour Ambre,
attention il y a des erreurs dans tes écris

Ambre a écrit :alors j'ai fait 2,5X2,5 = 6,25m2 qui est l'aire du carré après j'ai calculée le volume du cube 2,5 au cube = 15,625m3

Effectivement faut additionner les deux volumes et tu n'as pas de soustraction à faire.
Ensuite il te faut transformer les Litres en \(m^3\) et non \(cm^3\) puisque les unités sont des m (désolé j'avais mal lu)
Maintenant il te faut regarder si la quantité d'eau reste dans la partie pyramide où alors monte jusque dans le cube à partir de là il te faut faire un calcul pour trouver la hauteur ( une équation à résoudre). Essaye de te mettre en situation pour bien visualiser ce qui se passe.
Si ça monte jusque dans le cube tu connais déjà une partie de la hauteur....
Je te laisse faire les recherches.

Alors j'ai cherchée pour le petit 2 et j'ai pas trouvée un équation mais je me suis dit que si on prenait le volume total de la cuve et que l'on retiré 17,5 on trouverai la distance cet à dire 4,375m3. Ensuite je sais que vous m'avez expliquée pour l'exercice 2 mais je ne trouve pas en quoi rajouter la même figure peut nous aider a calculer le volume d'eau.

Bonjour Ambre,
tu mélanges le volume et la hauteur.
Quand tu verses du liquide dans la cuve, en premier se remplie la pyramide et si il y a suffisamment de liquide se rempli ensuite le cube.
Combien faut-il de liquide pour remplir en entier la pyramide, combien en reste t-il à verser dans le cube? Cette quantité de liquide correspond à quelle hauteur dans le cube?
Pour l'exercice 2 si tu as un pavé de dimension 12x25x2,2 quel solide dois tu enlever pour obtenir la piscine?

Donc on prend le volume de la pyramide qui est de 6,25 on prend donc 17,5-6,25 =11,25 et 17,25-11,25 = 6,25 le cube est donc remplis à 6,25 de hauteur et donc la on prend 21,878-6,25=15,628 le niveau de l'eau se trouve donc à 15,628 du bord de la cuve.

Pour la piscine on enlève le prisme qui mesure 8,80 et 2,20 de hauteur et 25 et 12 de largeur.

Ton début de raisonnement est juste à savoir que si on verse 17,5 \(m^3\) la pyramide est pleine et il reste 11,25 \(m^3\) à verser dans le cube.
Après tu mélange encore les \(m^3\) et les \(m\).
A partir de ce résultat il faut te poser la question j'ai un pavé de largeur 2,5\(m\) de longueur 2,5\(m\) et de hauteur \(x\)m. Quelle doit être la valeur de \(x\) pour qu'il contienne 11,25\(m^3\)
Quand tu auras trouvé la valeur de \(x\) ce sera le niveau de l'eau dans le cube, il te restera à calculer quelle hauteur il manque pour atteindre le haut de la cuve

Donc si je comprend bien on fait 2,5x +2,5 et à partir de la on résous l'équation. Je suis vraiment désolé de vous ennuyer.

Ambre a écrit :Pour la piscine on enlève le prisme qui mesure 8,80 et 2,20 de hauteur et 25 et 12 de largeur.

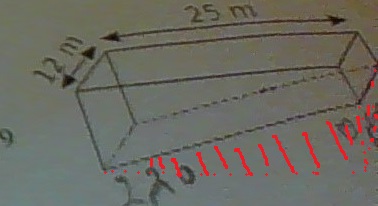
Pour la piscine si tu pars du pavé droit l = 12 ; L = 25 et H = 2,20 tu dois lui ôter une pyramide de base l = 1,4 ; L = 12 et H = 25 je sais pas si tu vois bien sur le schéma?

Ambre a écrit :Donc si je comprend bien on fait 2,5x +2,5 et à partir de la on résous l'équation. Je suis vraiment désolé de vous ennuyer.

\(2,5 \times 2,5 \times x = 11,25\)
A toi de terminer.

Je trouve 1,8 sa veut dire qu'il y a 1,8m3 d'eau donc on fait 3-1,8 =1,2 m3 l'eau se trouve a 1,2 m3 du bord.

Le résultat est juste mais pas ce que tu dis ensuite car ENCORE une fois c'est des \(m\) et pas des \(m^3\)
Les \(m\) c'est des longueurs et les \(m^3\) des volumes!!!!!
Reformule ta phrase avec \(m\) au lieu de \(m^3\)