Page 1 sur 1
Démonstration avec des vecteurs
Posté : sam. 27 févr. 2016 18:58
par Pauline
Bonsoir,
J'ai un petit soucis pour une démonstration de vecteurs...
Voici les données de l'énoncé :
BM= BA+BC
MP = 2MA
MN= 2MC
Avec cela, il faut démontrer :
PN = 2PB
J'ai vraiment du mal, quelqu'un peut m'aider ?
Merci !
NB: Les données si dessus sont des vecteurs, pas des longueurs, mais je ne sais pas mettre les flèches par informatique.
Re: Démonstration avec des vecteurs
Posté : sam. 27 févr. 2016 20:04
par sos-math(27)
Bonjour Pauline,
As tu commencé par faire un dessin représentant cette situation, cela aide ensuite pour écrire !
Le calcul à faire repose sur la relation de Chasles, te souviens tu l'avoir étudiée en classe ?
à bientôt
Re: Démonstration avec des vecteurs
Posté : dim. 28 févr. 2016 09:42
par Pauline
J'ai fait un desssin mais il me complique beaucoup le raisonnement...
Oui, bien sûr ! Avec ce calcul, j'ai essayé d'appliquer la relation de Chasles plein de fois, mais je n'aboutis jamais au résultat attendu.
Par exemple, j'ai écrit :
PN= PM + MN
PN= PB + BM + MN
PN= BP + BA + BC + 2MC
Et après cela, rien de très productif...
Re: Démonstration avec des vecteurs
Posté : dim. 28 févr. 2016 10:47
par sos-math(27)
Bonjour Pauline,
C'est pourtant la bonne méthode, mais tu dois garder comme objectif le résultat auquel tu veux aboutir.
Cela s'appelle la "décomposition" des vecteurs : l'idée est bien d'écrire un vecteur AB comme la somme de deux vecteurs AC+CB par exemple.
Ici tu connais : BM= BA+BC ; MP = 2MA ; MN= 2MC
et tu veux aboutir à une relation entre PN et PB.
Le dessin aide beaucoup à comprendre, je t'ai fait une représentation :
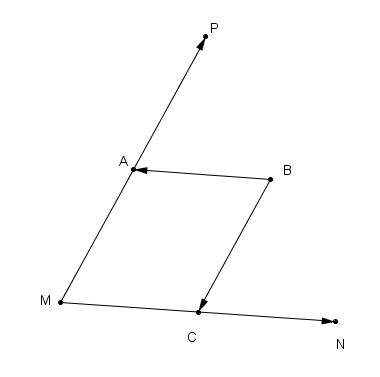
- vecteurs_2.PNG (7.04 Kio) Vu 5233 fois
Il faut donc 'décomposer' le vecteur PN en utilisant M et le vecteur PB en utilisant M... on va essayer d'arriver à utiliser ensuite uniquement les vecteurs MA et MC .
PN= PM + MN
PN= PB + BM + MN
PN= BP + BA + BC + 2MC
Tu étais bien partie à la ligne 1 ! Mais il faut utiliser maintenant les données : par quoi remplacer PM et MN ?
Re: Démonstration avec des vecteurs
Posté : dim. 28 févr. 2016 13:03
par Pauline
Eh bien, on peut mettre...
PN = PM+MN
PN = 2AM + 2MC
Et après il faut bien que je fasse apparaître le point P et B non ?
Re: Démonstration avec des vecteurs
Posté : dim. 28 févr. 2016 13:09
par sos-math(27)
Si on veut utiliser uniquement MA et MC, l'égalité que tu proposes n'est pas exacte ...
PN = 2AM + 2MC = .... MA -2 MC
Ensuite, faire intervenir le point M pour décomposer PB, et essayer de l'écrire seulement avec MA et MC . je reste à l'écoute
Re: Démonstration avec des vecteurs
Posté : dim. 28 févr. 2016 14:04
par Pauline
Je n'ai pas compris l'égalité énoncé juste avant...
Si on veut utiliser MA et MC uniquement il faudrait mettre
PN= -2MA +2 MC ?
Re: Démonstration avec des vecteurs
Posté : dim. 28 févr. 2016 14:23
par SoS-Math(31)
Bonjour Pauline,
oui, ton égalité était juste.
Maintenant, complétes ces égalités afin de faire intervenir le point B :
\(\overrightarrow{AM} = \overrightarrow{AB} + \overrightarrow{B...} et \overrightarrow{MC} = \overrightarrow{MB} + \overrightarrow{B...}\)
Re: Démonstration avec des vecteurs
Posté : dim. 28 févr. 2016 15:10
par sos-math(27)
Désolée Pauline,
Sos math 31 a une autre méthode, elle doit aussi aboutir au même résultat (c'est la beauté des maths) mais je persiste à te demander de décomposer PB avec le point M car c'est le vecteur qui t'es demandé.
PB = P... + ...B = .... tu peux continuer en utilisant la définition des vecteur et aussi le fait que MABC est un parallélogramme.
Je reste à l'écoute
Re: Démonstration avec des vecteurs
Posté : lun. 29 févr. 2016 12:16
par Pauline
D'accord... De toute façon, je suis ouverte à toutes les solutions possibles...
Je ne cible pas trop la méthode utilisée mais je vais faire mon possible pour poursuivre la démarche et trouver le résultat attendu.
Re: Démonstration avec des vecteurs
Posté : lun. 29 févr. 2016 13:40
par sos-math(27)
D'accord Pauline, je reste à l'écoute encore ce soir ...