Page 1 sur 1
Equation
Posté : mar. 23 déc. 2014 22:46
par Théo 2nde
Bonsoir,
Je suis bloqué à la résolution d'une équation:

- Maths.png (3.16 Kio) Vu 2951 fois
Merci d'avance.
Re: Equation
Posté : mer. 24 déc. 2014 12:09
par SoS-Math(9)
Bonjour Théo,
Pour la première équation : Il faut commencer par factoriser (7x-2)² - 9. Un peu d'aide : (7x-2)² - 9 = (7x-2)² - 3², tu as alors une différence de deux carrés.
Pour la deuxième, oui il faut factoriser par (7x-5) ...
(7x-5)(7x+1) = 3(7x-5)
<=> (7x-5)(7x+1) - 3(7x-5) = 0
On utilise alors la formule ka - kb = k(a-b) où k = (7x-5) (facteur commun) et a = ... et b = ... je te laisse compléter.
SoSMath.
Re: Equation
Posté : mer. 24 déc. 2014 21:06
par Théo 2nde
Bonsoir,
Merci de votre réponse, voici ce que j'ai fait:
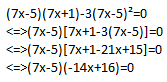
- Maths.png (2.1 Kio) Vu 2947 fois
je résous ensuite l'équation, est-ce cela ?
Merci d'avance.
Re: Equation
Posté : jeu. 25 déc. 2014 09:43
par SoS-Math(9)
Bonjour Théo,
C'est bien pour la factorisation.
Pour la résolution, voici un rappel : A x B = 0 <=> A = 0 ou B = 0.
SoSMath.
Re: Equation
Posté : ven. 26 déc. 2014 12:09
par Théo 2nde
Bonjour,
Merci, j'ai pu terminer. J'ai juste une dernière question pour cette équation:

- Maths.png (4.91 Kio) Vu 2940 fois
Merci d'avance.
Re: Equation
Posté : ven. 26 déc. 2014 13:07
par SoS-Math(25)
Bonjour Théo,
Es-tu sûr de ton équation ? Je ne trouve pas de factorisation simple ici.
A bientôt !
Re: Equation
Posté : ven. 26 déc. 2014 13:50
par Théo 2nde
Oui, je suis sur. Ou sinon je développe et je regarde le graphe. Et il semblerait que h(x)=f(x) ne soit pas possible...
Merci d'avance.
Re: Equation
Posté : ven. 26 déc. 2014 13:54
par SoS-Math(25)
Le graphe est une très bonne idée pour observer ce genre de résultat. Effectivement, il n'y a pas de solution réelle me semble-t-il.
A bientôt !
Re: Equation
Posté : ven. 26 déc. 2014 13:58
par Théo 2nde
Merci beaucoup.