Page 1 sur 1
Retrouver la fonction....
Posté : mer. 29 janv. 2014 18:36
par baszoe
Bonsoir,
Dans mon devoir je dois retrouver la fonction par rapport au valeur ci dessous et là je suis sec...
Pouvez vous me mettre sur la voie??
Fréquence F en hertz: 1770 1330 1060 890 760 670 590 525 480 440
longueur L en cm : 15 20 25 30 35 40 45 50 55 60
Dans l'attente de votre aide je vous remercie d'avance
Re: Retrouver la fonction....
Posté : mer. 29 janv. 2014 18:55
par SoS-Math(11)
Bonsoir,
Je te propose de mettre tes données dans un tableur, de faire un graphique en nuage de points et d'insérer une courbe de tendance et de faire afficher son équation. Cela donne une fonction du type K/x.
Bonne continuation
Re: Retrouver la fonction....
Posté : mer. 29 janv. 2014 19:27
par Invité
SoS-Math(11) a écrit :Bonsoir,
Je te propose de mettre tes données dans un tableur, de faire un graphique en nuage de points et d'insérer une courbe de tendance et de faire afficher son équation. Cela donne une fonction du type K/x.
Bonne continuation
merci pour votre réponse.
Mais je voudrais savoir comment faire pour trouver "cette fonction" sans utiliser de tableur par le calcul??
MERCI
Re: Retrouver la fonction....
Posté : mer. 29 janv. 2014 20:16
par SoS-Math(11)
Sans tableur, tu peux commencer par étudier les fonctions dites de référence : fonction affine, fonction carré, fonction cube et fonction inverse.
Ici tu vois que plus la longueur augmente plus la fréquence diminue donc on est dans le cas d'une fonction inverse.
En dehors de ces fonctions c'est plus difficile mais ce n'est pas du programme de seconde.
Bonne continuation
Re: Retrouver la fonction....
Posté : mer. 29 janv. 2014 21:04
par baszoe
Bonsoir,
Pourtant je suis en seconde. Je pense que je ne doit pas comprendre le sens de la question, je suis perdu...
Pouvez me dire comment faire pour traiter mon problème???
je vous joins la question.
merci encore pour votre aide.
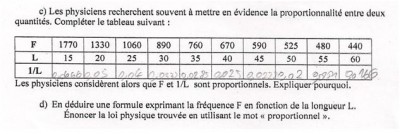
- Énoncé de math
Re: Retrouver la fonction....
Posté : mer. 29 janv. 2014 21:32
par SoS-Math(11)
Par définition : la proportionnalité entre deux grandeurs physiques \(G1\) et \(G2\) est traduite par la relation : \(G2 = k\times G1\).
Ici tu as à peu près, cela dépend des mesures effectuées, \(F = \frac{26550}{L}=26550\times \frac{1}{L}\) donc la fréquence est proportionnelle à l'inverse de L.
D'où le mot proportionnel. En math on utilise fonction associée à la fonction inverse (f(x)=1/x).
Bonne continuation