Page 1 sur 1
Cocinus d'un angle aigu dans un triangle rectangle.
Posté : mer. 13 avr. 2011 11:10
par Julie
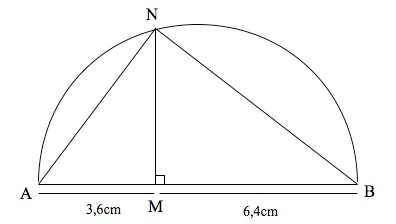
- Voici la figure
- Géométrie.jpg (12.29 Kio) Vu 2317 fois
Bonjour, je travaille avec le livre de Mathématique collection phare 4ème, et j'aurai besoin d'aide pour le n°58 page 244 :
Voici l'énoncé ;
1) Construire en vraie grandeur la figure ci-contre dans laquelle : Le point M appartient au segment [AB],
le point N appartient au demi-cercle de diamètre [AB].
2) Déterminez la valeur exacte de AN
3) En déduire une valeur approchée de la mesure de l'angle BAN .
J'ai donc démontrez que le triangle ANM était rectangle en N étant inscrit dans le demi-cercle de diamètre [AB]
Mais je suis bloquée pour trouver [AN], en revanche quand je l'aurai trouvé, je n'ai pas de problèmes pour la question 3.
Merci beaucoup
Julie
Re: Cocinus d'un angle aigu dans un triangle rectangle.
Posté : mer. 13 avr. 2011 13:54
par SoS-Math(1)
Bonjour Julie,
Il faut que tu exprimes \(\cos{\widehat{A}}\) de deux manières différentes en utilisant deux triangles rectangles différents.
A bientôt.
Re: Cocinus d'un angle aigu dans un triangle rectangle.
Posté : mer. 13 avr. 2011 14:11
par Julie
Donc j'utilise le triangle ANM et ça me donne :
Cos  = AM/AN
Et avec le triangle ANB ça donne
Cos  = AN/AB
Mais pour moi il manque toujours quelque chose puisque selon ANM,
Cos  = 3,6/AN et selon ANB Cos  = AN/10
Ah mais.. alors on peut faire une équation ? De sorte à trouver Cos  = AM/AB ? Donc 3,6/10 ?
Non je ne pense pas..
Re: Cocinus d'un angle aigu dans un triangle rectangle.
Posté : mer. 13 avr. 2011 14:16
par SoS-Math(1)
Bonjour Julie,
N'oublie pas de dire bonjour...
On obtient en effet une équation: \(\frac{3,6}{AN}=\frac{AN}{10}\).
"Le produit en croix": cela évoque-t-il quelque chose pour toi?
A bientôt.
Re: Cocinus d'un angle aigu dans un triangle rectangle.
Posté : mer. 13 avr. 2011 14:22
par Julie
Bonjour,
Merci beaucoup, cela m'a bien aidé, pour finir, pourriez-vous juste me dire si cette écriture est correcte ?
Dans le triangle AMN rectangle en M,
Cos  = AM/AN
Cos  = 3,6/AN
Dans le triangle ABN rectangle en N,
Cos  = AN/AM
Cos  = AN/ 10
Donc Cos  = AM/AN = AN/AM
= 3,6/10
Merci beaucoup.
Re: Cocinus d'un angle aigu dans un triangle rectangle.
Posté : mer. 13 avr. 2011 14:25
par SoS-Math(1)
Bonjour Julie,
Non, ce n'est pas correct à la fin.
Tu dois relire mon message précédent et faire le produit en croix.
A bientôt.
Re: Cocinus d'un angle aigu dans un triangle rectangle.
Posté : mer. 13 avr. 2011 15:04
par Julie
Bonjour,
Une fois que j'ai le cosinus, c'est à dire
Cos  = 3,6/10
Quand je cherche AN dans les deux triangles je ne trouve pas la même chose !
Ce qui est normal a priori mais je ne comprend pas pourquoi..
Dans le triangle ANB :
Cos  = AN/AB
AN = Cos  x AB
AN = 0,36 x 10
AN = 3,6
Dans le triangle ANM :
Cos  = AM/AN
AN x Cos  = AM
AN x O,36 = 3,6
AN = 3,6/0,36
AN = 10
Je comprend ce raisonnement mais alors comment trouver AN ?
Merci
Re: Cocinus d'un angle aigu dans un triangle rectangle.
Posté : mer. 13 avr. 2011 15:14
par SoS-Math(1)
Bonjour Julie,
Le cosinus de l'angle \(\widehat{A}\) n'est pas égal à 3,6/10.
Tu dois revoir cela.
Tu as tout ce qu'il te faut dans mon message de 15 h 16.
A bientôt.