Page 1 sur 1
exercice 1
Posté : sam. 17 avr. 2010 16:21
par Lolita
Bonjour, j' ai un exercice à faire, mais ca ne va malheureusement pas être possible. J' espère que vous pourrais m' aider:
Démontrer que dans la figure suivante (cos D)² + (cos K)²= 1
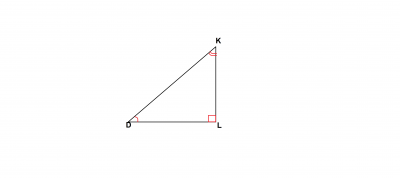
- Figure
Re: exercice 1
Posté : sam. 17 avr. 2010 19:55
par SoS-Math(1)
Bonjour Lolita,
\(\cos~\widehat{D}=\frac{DL}{DK}\) et \(\cos~\widehat{K}=\frac{KL}{DK}\).
Essayer maintenant de calculer \((\cos\widehat{D})^2+(\cos\widehat{K})^2\) en vous servant de ce que j'ai écrit plus haut.
A bientôt.
Re: exercice 1
Posté : dim. 18 avr. 2010 16:02
par Lolita
Re- bonjour, si DL² + KL²= DK² , (theoreme reciproque de pythagore). Donc (DL fois DL sur DK fois DK)+(KL fois KL sur DK fois DK) = 1.
J' aimerai savoir pourquoi ?
Au revoir et a bientot
Re: exercice 1
Posté : dim. 18 avr. 2010 18:00
par SoS-Math(2)
Bonjour
Vous avez compris que
\(DL^2+LK^2=DK^2\)
Si on divise à gauche et à droite par DK² alors
\(\frac{DL^2+LK^2}{DK^2}=\frac{DK^2}{DK^2}=1\)
bon courage