Page 1 sur 1
Dm sur les triangles et parallèles
Posté : sam. 21 févr. 2015 08:30
par Eléa
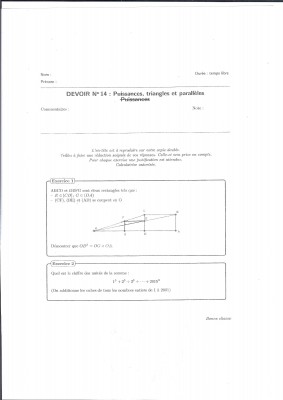
- dm 4ème exercice 1
Bonjour,
J'aurai besoin d'aide pour cet exercice de DM car je ne comprend pas comment on peut démontrer que OD au carré est égal à OG fois OA avec les propriétés des triangles et parallèles.
Si vous pouviez m'expliquer cet exercice ce serai gentil car je ne comprend pas trop.
Merci beaucoup d'avance.
cordialement,
Eléa.
Re: Dm sur les triangles et parallèles
Posté : sam. 21 févr. 2015 10:55
par SoS-Math(9)
Bonjour Eléa,
Dans ton exercice il s'agit d'utiliser la propriété de Thalès dans différentes configurations.
Il faut écrire la propriété de Thalès dans trois triangles.
SoSMath.
Re: Dm sur les triangles et parallèles
Posté : sam. 21 févr. 2015 18:41
par Eléa
Merci de votre réponse,
J'ai fait ce que vous m'avez dit, j'ai trouvé ces rapports là :
- Dans le triangle OED, (j'ai nommé I le point d'intersection de OB et FG)
OI OG IG
SUR = SUR = SUR
OE OD ED
- Dans le triangle OBA
OE OD ED
SUR= SUR = SUR
OB OA BA
- Et toujours dans le triangle OBA
OI OG IG
SUR= SUR = SUR
OB OA BA
Après j'ai vu que dans les 9 différents rapport, je trouve à chaque fois au milieu : OG SUR OD, OD SUR OA et OG SUR OA
j'ai mis que c'est 3 rapport était égal.
Mais après je suis bloqué, je ne sais pas comment continuer.
si vous pouviez m'aider.
je vous remercie d'avance.
Eléa.
Re: Dm sur les triangles et parallèles
Posté : sam. 21 févr. 2015 19:03
par SoS-Math(9)
Eléa,
Ce que tu as fait est juste. Cependant il y a plus simple en utilisant le triangle ODC. Mais reprenons tes rapports :
\(\fra{OI}{OE}=\frac{OG}{OD}\) alors \(OI=\frac{OG}{OD}\times OE\)
\(\fra{OI}{OB}=\frac{OG}{OA}\) alors \(OI=\frac{OG}{OA}\times OB\)
On a alors : \((OI=)\frac{OG}{OD}\times OE=\frac{OG}{OA}\times OB\).
Utilise alors ton dernier rapport ...
SoSMath.
Re: Dm sur les triangles et parallèles
Posté : mar. 24 févr. 2015 16:43
par Eléa
Bonjour, merci de votre aide.
Avec le dernier rapport cela fait : OE SUR OB = OD SUR OA alors OE= OD SUR OA fois OB
si je complète l’égalité que vous avez faites avec le dernier rapport je trouve : (OI=) OG SUR OD FOIS OD SUR OA FOIS OB = OG SUR OA FOIS OB.
j'ai remplacé OE par le dernier rapport que j'ai trouvé.
Après je ne comprend pas trop comment je peut arriver a la conclusion de OD au carré (qui fait OD FOIS OD) = OG FOIS OA.
Merci beaucoup, je vais continuer de chercher.
Eléa.
Re: Dm sur les triangles et parallèles
Posté : mer. 25 févr. 2015 08:25
par sos-math(21)
Bonjour,
je n'ai pas suivi votre méthode et je pense qu'il y a plus simple :
applique le théorème de Thalès dans le triangle OCD avec (FG)//(OD)
puis une deuxième fois thalès dans le triangle OBA avec (ED)//(AB).
Tu obtiens deux séries de rapports égaux dont un de la première série qui est égal à un autre de la deuxième série : il fait utiliser le fait qu'on a des rectangles.
Bon courage
Re: Dm sur les triangles et parallèles
Posté : mer. 25 févr. 2015 10:30
par Eléa
Bonjour, merci de votre réponse.
j'ai appliqué le théorème de Thalès dans ocd avec (FG)//(CD) : OF SUR OC = OG SUR OD= FG SUR CD
et dans OBA avec (ED)//(BA): OE SUR OB=OD SUR OA= ED SUR BA.
Je vois que je retrouve OD dans OG SUR OD et OD SUR OA.
si je fait je le produit en crois : OG SUR OD =OD SUR OA
OG = OD FOIS OD DIVISE PAR OA
OG = OD FOIS OD SUR OA
OG = OD au carré SUR OA
OD AU CARRE = OG FOIS OA sur 1
donc OG FOIS OA = OD au carré.
je pense que c'est ça.
merci de votre aide.
Eléa.
Re: Dm sur les triangles et parallèles
Posté : mer. 25 févr. 2015 12:04
par SoS-Math(9)
Bonjour Eléa.
Cela semble correct.
SoSMath.
Re: Dm sur les triangles et parallèles
Posté : ven. 27 févr. 2015 11:44
par Eléa
Merci beaucoup de votre aide.
A bientôt peut être.
Eléa.