- Figure
Bonsoir.
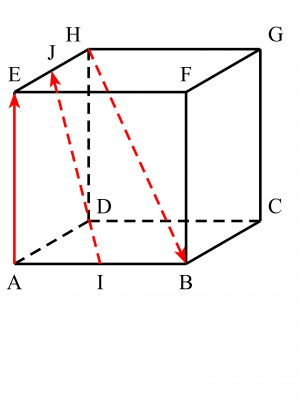
Je vous joins la figure de mon exercice.
Je dois montrer que les vecteurs AE, HB, IJ sont coplanaires en sachant que :
IJ = AE + 1/2BD (en vecteurs)
2IJ = AE - HB (en vecteurs)
Je n'ai aucune idée de la manière qu'il faut procéder.
Merci d'avance pour votre aide.
[attachment=0]image.png[/attachment]Bonsoir.
Je vous joins la figure de mon exercice.
Je dois montrer que les vecteurs AE, HB, IJ sont coplanaires en sachant que :
IJ = AE + 1/2BD (en vecteurs)
2IJ = AE - HB (en vecteurs)
Je n'ai aucune idée de la manière qu'il faut procéder.
Merci d'avance pour votre aide.