par Hugo » lun. 21 oct. 2013 10:32
Bonjour à tous !
Alors voilà, j'ai un DM pour les vacances, et je n'y arrive pas tellement. Le voici, avec l'image qui va avec:
1. Montrer que la limite de \(\frac{sin x}{x}\) en 0 présente une forme indéterminée.
-> Je pense avoir réussi, car \(\lim\limits_{x \to 0} sin x=0\) et \(\lim\limits_{x \to 0} x=0\) d'ou forme indéterminée du type \(\frac{0}{0}\)
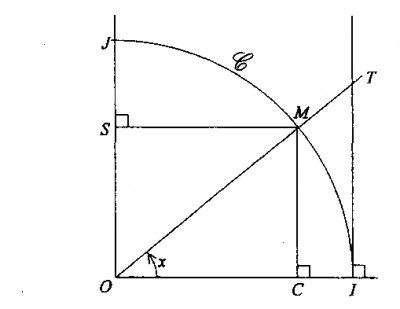
Soit x un réel de \(]0;\frac{\pi}{2}[\) et M le point du cercle trigonométrique tel que l'angle \((\overrightarrow{OI},\overrightarrow{OM})\) soit de mesure x (en radians).
2.
2.1. Exprimer, en fonction de x, la distance OC.
-> J'ai trouvé. On a d'après l'image: \(C(cosx; 0)\). Comme O est l'origine du repère, on a donc: \(OC=\sqrt{(cos x-0)^2+(0-0)^2}=cos x\)
2.2. Exprimer, en fonction de x, la distance OS.
-> On a également \(S(0;sin x)\). D'où \(OS=\sqrt{(0-0)^2+(sin x-0)^2}=sin x\)
2.3. Exprimer, en fonction de x, la distance IT.
-> On a \(OI=1\) car c'est un cercle trigonométrique et le rayon est OI. Je bloque un peu. Je pense que le triangle OIT est rectangle en I, mais je ne vois pas comment le démontrer. Je sais que je dois trouver que \(IT=tan x=\frac{sin x}{cos x}=\frac{OS}{OC}\). Mais pourquoi ?
2.4. Exprimer, en fonction de x, l'aire \(a_1\) du triangle OIM.
-> Assez simple: \(a_1=\frac{base\times hauteur}{2}=\frac{OI\times CM}{2}\). Après je pense que on a \(CM=OS\) mais je ne sais plus comment on le démontre. Je ne vois pas non plus pourquoi CM est une hauteur. C'est une propriété trigonométrique ?
D'où \(a_1=\frac{OI\times OS}{2}=\frac{sin x}{2}\)
2.5. Exprimer, en fonction de x, l'aire \(a_2\) du secteur angulaire IOM.
-> J'ai dû me renseigner sur les secteurs angulaires (je ne savais pas ce que c'était) et j'ai donc \(a_2=\frac{x}{2}\times R^2\) or le rayon vaut 1, donc \(a_2=\frac{x}{2}\)
2.6. Exprimer, en fonction de x, l'aire \(a_3\) du triangle OIT.
-> \(a_3=\frac{OI\times IT}{2}=\frac{tan x}{2}\). Evidemment ça ne marche que i je prouve que IT est perpendiculaire à OI.
3. En remarquant que \(a_1\le a_2\le a_3\), donnez un encadrement de \(\frac{sin x}{x}\) sur \(]0;\frac{\pi}{2}[\).
En déduire \(\lim\limits_{x \to 0^+} \frac{sin x}{x}\)
-> On a donc \(\frac{sin x}{2}\le \frac{x}{2}\le \frac{tan x}{2}\)
Soit \(sin x\le x\le tan x\)
D'où \(\frac{(sin x)^2}{x}\le \frac{sin x}{x}\le \frac{tan xsin x}{x}\).
Je ne sais pas quoi faire après. Je me doute qu'on va devoir utiliser le théorème des gendarmes.
4. En utilisant la parité de \(\frac{sin x}{x}\), en déduire \(\lim\limits_{x \to 0^-} \frac{sin x}{x}\)
-> N'ayant pas trouvé la question précédente, je ne pense pas pouvoir résoudre celle-ci.
Cependant, si on utilise la parité, on aurait:
\(\frac{sin (-x)}{-x}=\frac{-sin x}{-x}=\frac{sin x}{x}\)
Donc voilà, si vous pouviez m'aider (pas me donner de solution, s'il-vous-plait, je cherche vraiment à comprendre...) je vous en remercierait grandement :) !
Je pense aussi que je n'arrive pas à avancer suite à des lacunes de définitions trigonométriques.
Bonne journée !
- Fichiers joints
-
Bonjour à tous !
Alors voilà, j'ai un DM pour les vacances, et je n'y arrive pas tellement. Le voici, avec l'image qui va avec:
[b]1. Montrer que la limite de [tex]\frac{sin x}{x}[/tex] en 0 présente une forme indéterminée.[/b]
-> Je pense avoir réussi, car [tex]\lim\limits_{x \to 0} sin x=0[/tex] et [tex]\lim\limits_{x \to 0} x=0[/tex] d'ou forme indéterminée du type [tex]\frac{0}{0}[/tex]
[i]Soit x un réel de [tex]]0;\frac{\pi}{2}[[/tex] et M le point du cercle trigonométrique tel que l'angle [tex](\overrightarrow{OI},\overrightarrow{OM})[/tex] soit de mesure x (en radians).[/i]
[b]2.
2.1. Exprimer, en fonction de x, la distance OC.[/b]
-> J'ai trouvé. On a d'après l'image: [tex]C(cosx; 0)[/tex]. Comme O est l'origine du repère, on a donc: [tex]OC=\sqrt{(cos x-0)^2+(0-0)^2}=cos x[/tex]
[b]2.2. Exprimer, en fonction de x, la distance OS.[/b]
-> On a également [tex]S(0;sin x)[/tex]. D'où [tex]OS=\sqrt{(0-0)^2+(sin x-0)^2}=sin x[/tex]
[b]2.3. Exprimer, en fonction de x, la distance IT.[/b]
-> On a [tex]OI=1[/tex] car c'est un cercle trigonométrique et le rayon est OI. Je bloque un peu. Je pense que le triangle OIT est rectangle en I, mais je ne vois pas comment le démontrer. Je sais que je dois trouver que [tex]IT=tan x=\frac{sin x}{cos x}=\frac{OS}{OC}[/tex]. Mais pourquoi ?
[b]2.4. Exprimer, en fonction de x, l'aire [tex]a_1[/tex] du triangle OIM.[/b]
-> Assez simple: [tex]a_1=\frac{base\times hauteur}{2}=\frac{OI\times CM}{2}[/tex]. Après je pense que on a [tex]CM=OS[/tex] mais je ne sais plus comment on le démontre. Je ne vois pas non plus pourquoi CM est une hauteur. C'est une propriété trigonométrique ?
D'où [tex]a_1=\frac{OI\times OS}{2}=\frac{sin x}{2}[/tex]
[b]2.5. Exprimer, en fonction de x, l'aire [tex]a_2[/tex] du secteur angulaire IOM.[/b]
-> J'ai dû me renseigner sur les secteurs angulaires (je ne savais pas ce que c'était) et j'ai donc [tex]a_2=\frac{x}{2}\times R^2[/tex] or le rayon vaut 1, donc [tex]a_2=\frac{x}{2}[/tex]
[b]2.6. Exprimer, en fonction de x, l'aire [tex]a_3[/tex] du triangle OIT.[/b]
-> [tex]a_3=\frac{OI\times IT}{2}=\frac{tan x}{2}[/tex]. Evidemment ça ne marche que i je prouve que IT est perpendiculaire à OI.
[b]3. En remarquant que [tex]a_1\le a_2\le a_3[/tex], donnez un encadrement de [tex]\frac{sin x}{x}[/tex] sur [tex]]0;\frac{\pi}{2}[[/tex].
En déduire [tex]\lim\limits_{x \to 0^+} \frac{sin x}{x}[/tex][/b]
-> On a donc [tex]\frac{sin x}{2}\le \frac{x}{2}\le \frac{tan x}{2}[/tex]
Soit [tex]sin x\le x\le tan x[/tex]
D'où [tex]\frac{(sin x)^2}{x}\le \frac{sin x}{x}\le \frac{tan xsin x}{x}[/tex].
Je ne sais pas quoi faire après. Je me doute qu'on va devoir utiliser le théorème des gendarmes.
[b]4. En utilisant la parité de [tex]\frac{sin x}{x}[/tex], en déduire [tex]\lim\limits_{x \to 0^-} \frac{sin x}{x}[/tex][/b]
-> N'ayant pas trouvé la question précédente, je ne pense pas pouvoir résoudre celle-ci.
Cependant, si on utilise la parité, on aurait:
[tex]\frac{sin (-x)}{-x}=\frac{-sin x}{-x}=\frac{sin x}{x}[/tex]
Donc voilà, si vous pouviez m'aider (pas me donner de solution, s'il-vous-plait, je cherche vraiment à comprendre...) je vous en remercierait grandement :) !
Je pense aussi que je n'arrive pas à avancer suite à des lacunes de définitions trigonométriques.
Bonne journée !