par Ledeyna » mar. 31 mars 2015 19:40
Bonsoir, J'ai un devoir maison assez urgent mais je n'arrive pas.. Pourriez-vous m'aider s'il vous plait?
Consigne de l'exercice 1:
"Dans le quadrilatère ci-dessous, le point O est le milieu de la diagonale [IJ].
1) Démontrer que : KO=LO.
2) Peut-on en déduire que le point O est le milieu du segment [KL]?
Justifier la réponse"
Consigne de l'exercice 2 :
"1)Construire un triangle EDC tel que:
ED=3,9 cm, EC=5,2 cm et DC=6,5 cm.
2) Calculer le rayob de son cercle circonscrit (mais comment). Justifier la réponse
Merci d'avance!!
- Fichiers joints
-
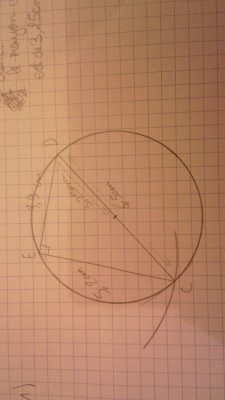
- Exercice 2: Calculer le rayon de son cercle circonscrit. Justifier
-
![1427830287835.jpg (1.34 Mio) Vu 1969 fois Exercice 1: Comment déduire que le point O est le milieu du segment [KL]? Justifier](./download/file.php?id=4125&t=1)
- Exercice 1: Comment déduire que le point O est le milieu du segment [KL]? Justifier
Bonsoir, J'ai un devoir maison assez urgent mais je n'arrive pas.. Pourriez-vous m'aider s'il vous plait?
Consigne de l'exercice 1:
"Dans le quadrilatère ci-dessous, le point O est le milieu de la diagonale [IJ].
1) Démontrer que : KO=LO.
2) Peut-on en déduire que le point O est le milieu du segment [KL]?
Justifier la réponse"
Consigne de l'exercice 2 :
"1)Construire un triangle EDC tel que:
ED=3,9 cm, EC=5,2 cm et DC=6,5 cm.
2) Calculer le rayob de son cercle circonscrit (mais comment). Justifier la réponse
Merci d'avance!!