par titi97434 » lun. 19 janv. 2015 12:01
Bonjour, j'ai un exercice de maths que je n'arrive pas à faire. Le voici:
"On a vu dans l'exercice 65 que le quadrilatère reliant les milieux des côtés d'un quadrilatère quelconque est un parallélogramme. Inversement, étant donné un parallélogramme, on peut construire un quadrilatère quelconque dont les sommets sont les milieux des côtés du quadrilatère quelconque.
1) Construire sur une feuille blanche un parallélogramme ABCD tel que: AB= 5 cm, AH= 3 cm et l'angle ABC= 50°.
2) Construire un quadrilatère IJKL tel que les points A, B, C et D soient les milieux respectifs des côtés IJ, JK, KL et LI.
3) Démontrer l'aire de IJKL.
J'ai fait la figure (voir l'illustration ci-dessous) mais je n'arrive pas à démontrer l'aire de IJKL. Au début, je voulais calculer l'aire du parallélogramme puis celles des triangles DIA, AJB, BKC et CLD. Mais pour calculer l'aire des triangles j'ai besoin de leurs hauteurs, or, je ne les ai pas. C'est à ce moment là que je bloque.
Après j'avais pensé aussi faire un découpage de la figure avec les propriétes de la droite des milieux: M milieu de IK (J'ai rajouté le point M) , montrer que les 4 triangles bleus ont même aire et idem pour les triangles rouges et montrer que la somme des aires des deux triangles rouge et bleu foncés est égale à la moitié de l'aire de ABCD.
Si vous pourriez me dire laquelle des deux techniques je devrais utiliser ou si vous en trouvez une autre (théorème de Thalès ?), je vous serez reconnaissante de me la transmettre :)
Merci d'avance pour votre aide
- Fichiers joints
-
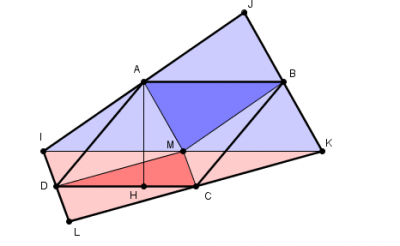
- Voici la figure ! :)
Bonjour, j'ai un exercice de maths que je n'arrive pas à faire. Le voici:
"On a vu dans l'exercice 65 que le quadrilatère reliant les milieux des côtés d'un quadrilatère quelconque est un parallélogramme. Inversement, étant donné un parallélogramme, on peut construire un quadrilatère quelconque dont les sommets sont les milieux des côtés du quadrilatère quelconque.
1) Construire sur une feuille blanche un parallélogramme ABCD tel que: AB= 5 cm, AH= 3 cm et l'angle ABC= 50°.
2) Construire un quadrilatère IJKL tel que les points A, B, C et D soient les milieux respectifs des côtés IJ, JK, KL et LI.
3) Démontrer l'aire de IJKL.
J'ai fait la figure (voir l'illustration ci-dessous) mais je n'arrive pas à démontrer l'aire de IJKL. Au début, je voulais calculer l'aire du parallélogramme puis celles des triangles DIA, AJB, BKC et CLD. Mais pour calculer l'aire des triangles j'ai besoin de leurs hauteurs, or, je ne les ai pas. C'est à ce moment là que je bloque.
Après j'avais pensé aussi faire un découpage de la figure avec les propriétes de la droite des milieux: M milieu de IK (J'ai rajouté le point M) , montrer que les 4 triangles bleus ont même aire et idem pour les triangles rouges et montrer que la somme des aires des deux triangles rouge et bleu foncés est égale à la moitié de l'aire de ABCD.
Si vous pourriez me dire laquelle des deux techniques je devrais utiliser ou si vous en trouvez une autre (théorème de Thalès ?), je vous serez reconnaissante de me la transmettre :)
Merci d'avance pour votre aide