par eleve16 » ven. 9 mars 2012 10:01
Bonjour,
Désolé de m'avoir mal exprimer ( je n'arrive plus a écrire sur le message d'avant alors je vous en écris un nouveau )
Tout simplement ce que je ne comprends pas c'est que dans l'exercice ils veulent qu'on calcule l'Aire alors qu'il n'y a pas de mesure.
Je réécris l'énoncé pour que vous l'ayez sous les yeux
voici l'énoncé:
Le théorème de Thalès démontré par Euclide.
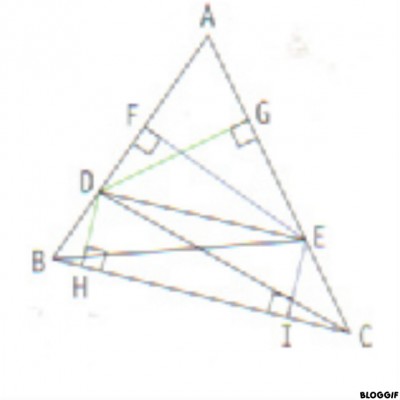
On veut démontrer la propriété de Thalès dans le triangle ABC.
Le point E appartient au segment [AC] et le point D au segment [AB]
tels que les droites (DE) et (BC) sont parallèles.
Les points F et I sont les pieds des hauteurs issues du point E respectivement
dans les triangles ADE et EBC.
Les points G et H sont les pieds des hauteurs issues du point D respectivement dans les triangles ADC et BDC.
a) Exprimer les aires des triangles ADE et ADC en fonction de DG, puis démontrer que: Aire ADE =AE.
Aire ADC AC
b)Démonterr de même que: Aire ADE=AD.
Aire ABE AB
c)Démontrer que Aire DBC = Aire BEC. Que peut-on en déduire pour les aires des triangle ABE et ADC ?
d)Déduire des questions précédentes que AE=AD.
AC AB
e)J est un point du segment [BC] tel que les droites (DJ) et (AC) sont parallèles.
Faire une figure, puis en s'inspirant de la méthode précédente, démontrer que
BD=BJ
BA BC
f)En exprimant BD en fonction de AD et AB, puis BJ en fonction de JC et BC, démontrer que AD=JC
AB BC
g)démontrer que JC=DE, puis en déduire que:
AE=AD=DE.
AC AE BC
Merci d'avance et encore désolé
Au revoir.
- Fichiers joints
-
- Figure
Bonjour,
Désolé de m'avoir mal exprimer ( je n'arrive plus a écrire sur le message d'avant alors je vous en écris un nouveau )
Tout simplement ce que je ne comprends pas c'est que dans l'exercice ils veulent qu'on calcule l'Aire alors qu'il n'y a pas de mesure.
Je réécris l'énoncé pour que vous l'ayez sous les yeux
voici l'énoncé:
Le théorème de Thalès démontré par Euclide.
On veut démontrer la propriété de Thalès dans le triangle ABC.
Le point E appartient au segment [AC] et le point D au segment [AB]
tels que les droites (DE) et (BC) sont parallèles.
Les points F et I sont les pieds des hauteurs issues du point E respectivement
dans les triangles ADE et EBC.
Les points G et H sont les pieds des hauteurs issues du point D respectivement dans les triangles ADC et BDC.
a) Exprimer les aires des triangles ADE et ADC en fonction de DG, puis démontrer que: Aire ADE =AE.
Aire ADC AC
b)Démonterr de même que: Aire ADE=AD.
Aire ABE AB
c)Démontrer que Aire DBC = Aire BEC. Que peut-on en déduire pour les aires des triangle ABE et ADC ?
d)Déduire des questions précédentes que AE=AD.
AC AB
e)J est un point du segment [BC] tel que les droites (DJ) et (AC) sont parallèles.
Faire une figure, puis en s'inspirant de la méthode précédente, démontrer que
BD=BJ
BA BC
f)En exprimant BD en fonction de AD et AB, puis BJ en fonction de JC et BC, démontrer que AD=JC
AB BC
g)démontrer que JC=DE, puis en déduire que:
AE=AD=DE.
AC AE BC
Merci d'avance et encore désolé
Au revoir.